W maju 2023 r. po raz pierwszy została sfotografowana Warszawa z Gór Świętokrzyskich, z odległości ponad 150 km. Najpierw 22 maja Paweł Kłak zaobserwował światło iglicy Varso Tower, a potem 28 maja udało się udokumentować panoramę 11 najwyższych budowli w stolicy (Łukasz Wawrzyszko i Paweł Kłak), po czym dzień później powtórzył to Kamil Gołąb.

Zdjęcia zostały szeroko udostępnione w internecie, po czym pojawiło się wiele sceptycznych komentarzy, podających w wątpliwość możliwość takiej obserwacji.
Czy taki widok jest możliwy mimo krzywizny Ziemi?
Oczywiście tak. Proste kalkulatory zakrzywienia Ziemi, używane do prób udowodnienia niemożliwości takiego widoku na kulistej planecie, nie uwzględniają ukształtowania terenu na linii obserwacji ani zjawisk optycznych związanych z propagacją światła w atmosferze.
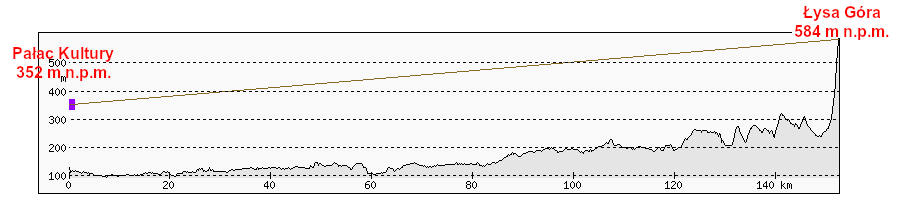
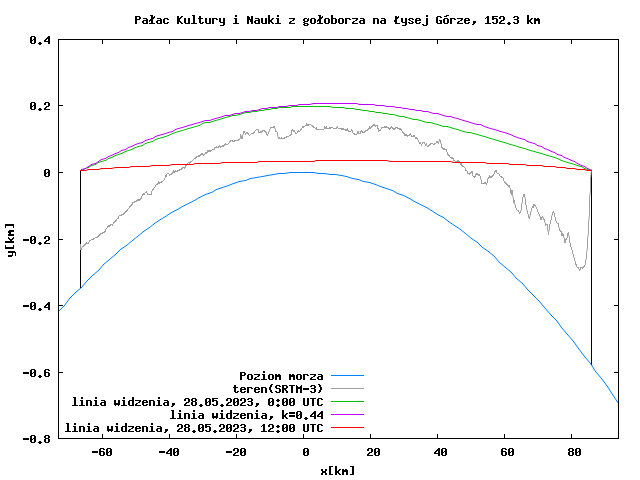
Poniższa ilustracja przedstawia profil ukształtowania terenu pomiędzy Łysą Górą a Pałacem Kultury i Nauki, z uwzględnieniem krzywizny Ziemi. Dla lepszej czytelności wysokość została przedstawiona w większej skali niż odległość (zgodnie z oznaczeniami osi), dlatego zarówno rzeźba terenu, jak i krzywizna Ziemi są powiększone.
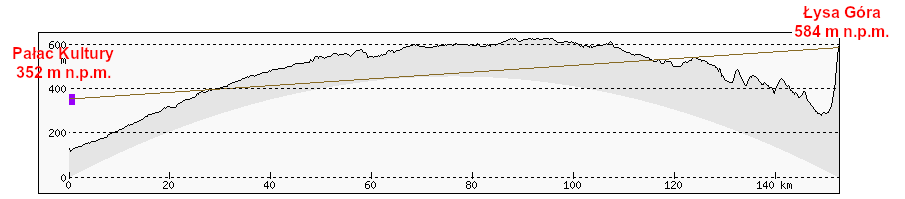

Brązowa linia jest to prosta linia biegnąca pomiędzy szczytem iglicy Pałacu Kultury i Nauki (wysokość 352 m n.p.m.) a obserwatorem pod szczytem Łysej Góry (584 m n.p.m.). Widać, że przecina ona teren znajdujący się po drodze – do widoczności brakuje bardzo dużo. Po linii prostej światło rozchodzi się jednak w próżni, a w niejednorodnym ośrodku, jakim jest ziemska atmosfera, jest inaczej. Im wyżej, tym ciśnienie atmosferyczne jest niższe, a powietrze ma mniejszą gęstość – a im rzadsze powietrze, tym mniejszy jest jego współczynnik załamania. Powietrze załamuje więc światło w taki sposób, że promienie światła zakrzywiają się w kierunku Ziemi (wypukłość krzywizny jest skierowana w kierunku mniejszego współczynnika załamania) – jest to zjawisko refrakcji atmosferycznej. Fizyczne i matematyczne szczegóły tego fenomenu są opisane na stronie Waltera Bislina.
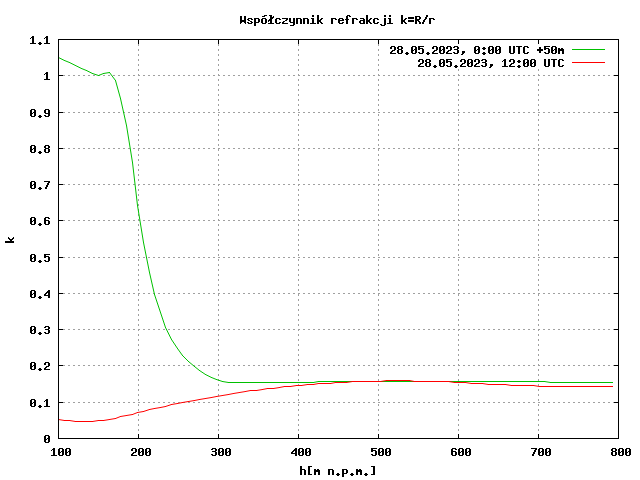
W standardowych warunkach promień krzywizny linii widzenia jest ok. 7 razy większy niż promień krzywizny kuli ziemskiej. Określa się to za pomocą współczynnika refrakcji zdefiniowanego jako iloraz promienia Ziemi oraz promienia tej krzywizny – wynosi on ok. 0,14 i na ogół w ciągu dnia ulega niewielkim zmianom m.in. w zależności od temperatury powietrza.
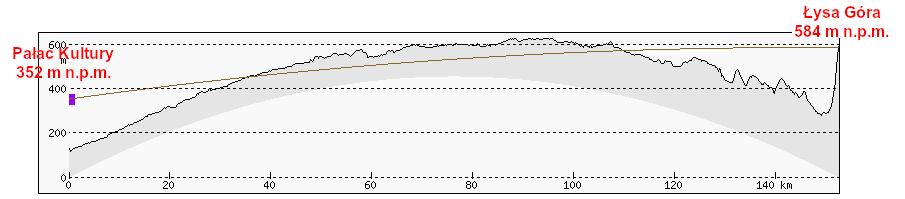
Po uwzględnieniu standardowej refrakcji widoczność nadal nie jest możliwa. Linia powędrowała nieco wyżej, lecz brakuje kilkudziesięciu metrów, by wyszła powyżej terenu zasłaniającego widok.
W pogodne noce grunt szybko wypromieniowuje ciepło, a wraz z nim ochładza się przygruntowa warstwa powietrza. Staje się ona zimniejsza od powietrza położonego wyżej – powstaje radiacyjna inwersja temperatury. Chłodniejsze powietrze jest gęstsze i ma wyższy współczynnik załamania – w takich warunkach zmiany współczynnika załamania są zatem większe niż zwykle i to dość znacznie. W warstwie powietrza o grubości kilkudziesięciu metrów różnica temperatur może wynosić kilka stopni Celsjusza. Światło załamuje się wtedy kilkakrotnie silniej niż standardowo. Sprawdźmy więc przebieg linii widzenia dla współczynnika refrakcji 0,4 – około 3 razy większego niż standardowy.
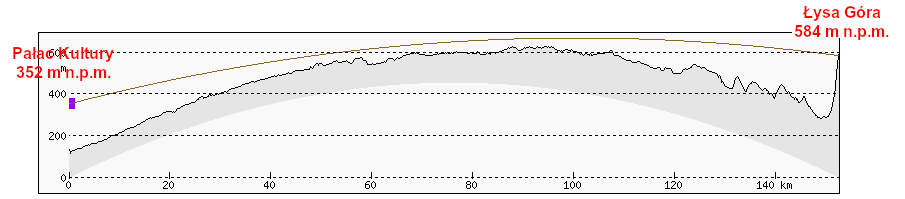
Skąd wiadomo, że 28 maja 2023 r. wystąpiła taka inwersja? Jej obecność potwierdzają pomiary sondażowe atmosfery wykonane za pomocą balonu meteorologicznego – najbliższy pomiar był wykonany w Legionowie o godz. 2 w nocy.
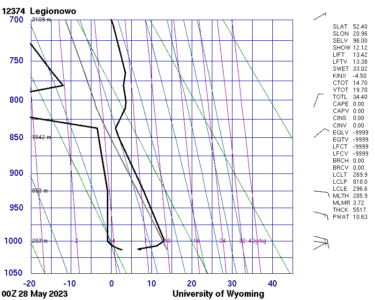
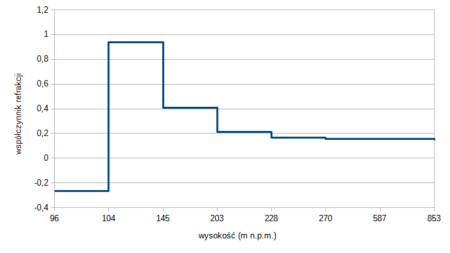
Inwersja temperatury w Legionowie wystąpiła w zakresie wysokości 104 – 203 m n.p.m., czyli ok. 10 – 110 m nad ziemią (prawdopodobnie sięgała nieco wyżej, gdyż na 203 i 228 m n.p.m. była identyczna temperatura). Nie mamy danych z linii Warszawa – Łysa Góra, więc nie da się określić dokładnego rozkładu tego współczynnika na linii obserwacji, ale warunki pogodowe były podobne, więc z pewnością również tam była inwersja. Linia widzenia tylko na części dystansu przechodziła przez warstwę inwersyjną, dlatego średni współczynnik refrakcji jest znacznie niższy niż maksymalne wartości. Najniższy widoczny na zdjęciach obiekt w Warszawie to światło na maszcie na budynku Centrum LIM, którego szczyt sięga 295 m n.p.m. Za pomocą opisanej tutaj metody można wyznaczyć minimalny średni współczynnik refrakcji, przy którym powinno być ono widoczne. Wynosi on ok. 0,44, więc co najmniej taka średnia jego wartość musiała wtedy wystąpić.
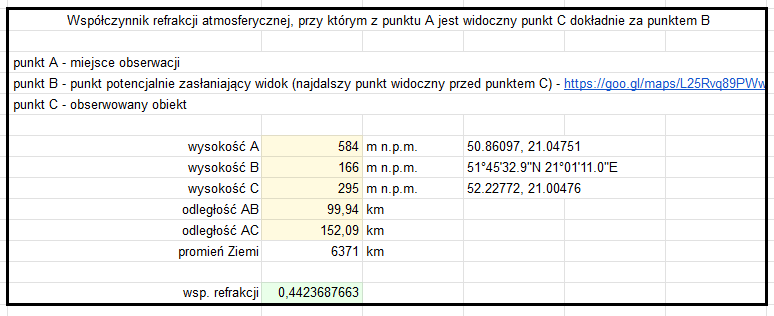
Powyższe analizy zakładają uproszczenie polegające na uśrednieniu współczynnika refrakcji dla całej linii widzenia. W przypadku inwersji obejmującej niewielki zakres wysokości zmienność refrakcji jest jednak na tyle duża, że rzeczywista linia widzenia w istotnym stopniu odbiega od uproszczonej.
Przy pomocy specjalnego programu analizującego rozchodzenie się światła w atmosferze o określonym pionowym profilu temperatury można wyznaczyć linię widzenia w danych warunkach.
Poniższe wykresy zostały opracowane przez dr. hab. Krzysztofa Strasburgera w oparciu o pomiary z Legionowa – dokładny opis na jego stronie.
A jak wyglądałoby to, gdyby Ziemia była płaska?
Oczywiście można coś takiego zasymulować za pomocą dostępnych programów.
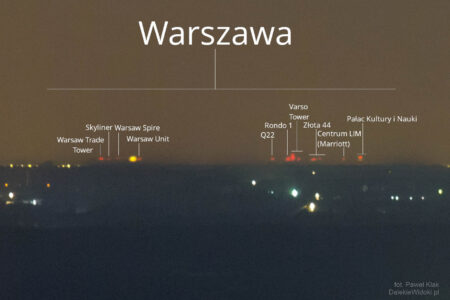
Skąd wiadomo, że skupisko czerwonych punktów na horyzoncie to właśnie Warszawa?
Są one widoczne dokładnie w tych miejscach, gdzie powinny znajdować się najwyższe warszawskie budynki. Azymut każdego z nich dokładnie pasuje do położenia na zdjęciu. Można go wyznaczyć z dużą dokładnością w następujący sposób.
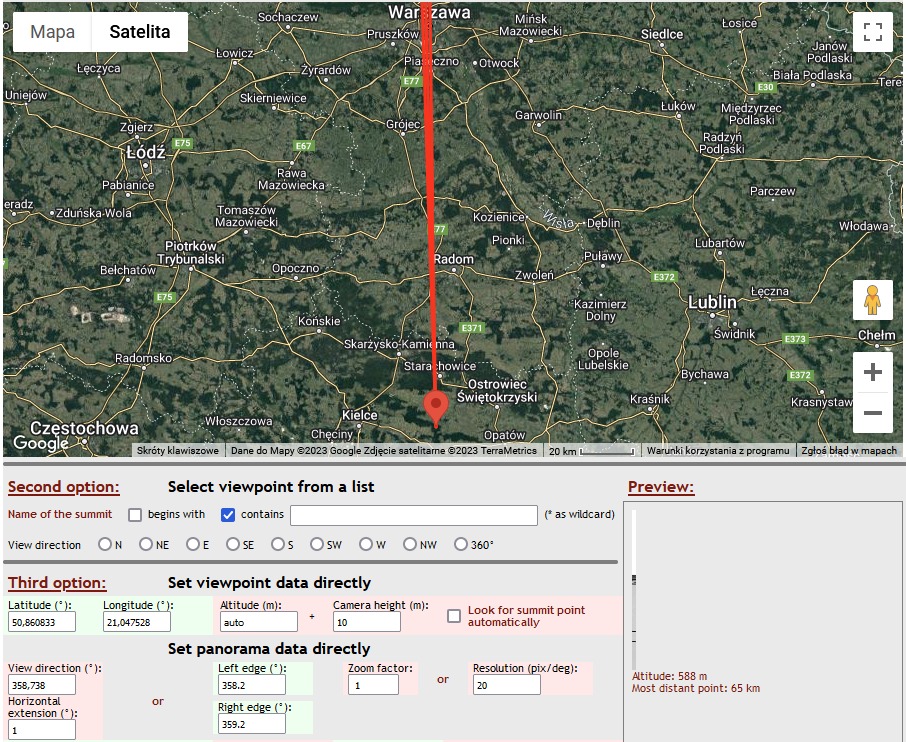
Po obu stronach Warszawy widać na zdjęciu wieże telefonii komórkowej z wyraźnymi czerwonymi światłami. Znając ich lokalizacje, można obliczyć azymuty do nich (np. kalkulatorem online).
Po lewej znajduje się wieża w Krogulczy Suchej (51,328411°N, 21,013814°E), a po prawej podobny obiekt w miejscowości Augustów (51,359309°N, 21,047798°E – nieoznaczony na mapie Google, ale widoczny na nowszej fotomapie w Geoportalu). Zdjęcie zostało zrobione z punktu 50,860833°N, 21,047528°E. Po wprowadzeniu współrzędnych do kalkulatora azymutów otrzymujemy azymuty: 357,420° do wieży w Krogulczy Suchej i 0,019° do Augustowa.
Następnie mierzymy poziomą odległość między wieżami na zdjęciu (w pikselach), dzielimy ją przez odległość kątową między nimi (różnicę azymutów) i otrzymujemy liczbę pikseli, jaka odpowiada na zdjęciu jednemu stopniowi kątowemu. Odległość na zdjęciu wynosi 4134 piksele, odległość kątowa to 360° – (357,420° – 0,019°) = 2,599°, a zatem jednemu stopniowi odpowiada na zdjęciu 4134 / 2,599 ≈ 1590,6 pikseli. Można teraz nanieść na zdjęcie podziałkę wyskalowaną w stopniach lub jego częściach (np. 0,1° co ok. 159 pikseli).
Taka podziałka ułatwia odczytanie azymutu do dowolnego obiektu – wystarczy zmierzyć, o ile pikseli jest oddalony w poziomie od najbliższej linii podziałki.

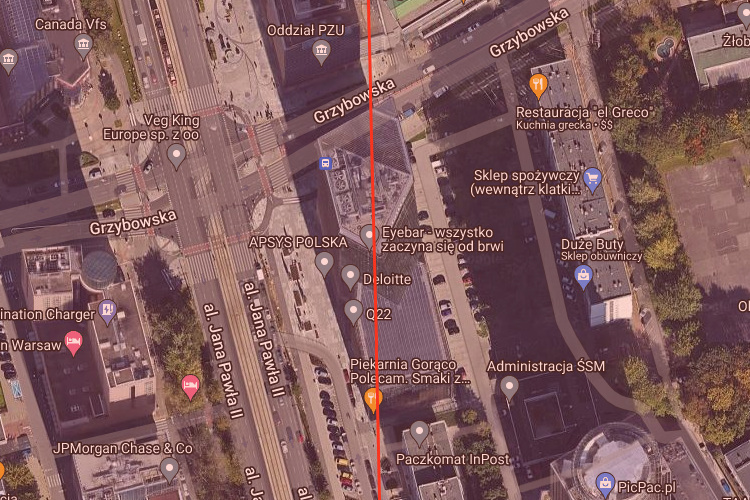
Na powyższym zdjęciu pokazano pomiar azymutu do jednego ze świecących obiektów. Jest on położony o 57 pikseli w prawo od azymutu 358,7°, czyli na azymucie 358,7 + 57/159 = 358,738°.
Teraz wystarczy poprowadzić na mapie linię biegnącą w tym właśnie kierunku – umożliwia to np. strona udeuschle.de. Linia trafia dokładnie na wieżowiec Q22 w Warszawie. Jest to jedyny wysoki obiekt na tej linii, co można sprawdzić na mapie przeszkód lotniczych, zawierającej lokalizacje obiektów o wysokości co najmniej 100 m.
W ten sam sposób można zidentyfikować kolejne obiekty. Azymuty do nich obliczone wyżej wspomnianym kalkulatorem przedstawia tabela:
| Obiekt | Mapa | Wysokość (m n.p.m.) | Azymut (°) | Odległość (km) |
| Widok z punktu 50,860972°N, 21,047500°E | ||||
| Warsaw Trade Tower | https://goo.gl/maps/XybUH5vUKPYWNpQE8 | 319 | 358,342 | 152,9 |
| Skyliner | https://goo.gl/maps/AhaBtLGHfPhFWfx9A | 307 | 358,359 | 152,3 |
| Warsaw Spire | https://goo.gl/maps/Tj1ELZChwgVuBGm29 | 331 | 358,377 | 152,5 |
| Warsaw Unit | https://goo.gl/maps/DND4F6zQa2B4d4PD7 | 316 | 358,429 | 152,3 |
| Q22 | https://goo.gl/maps/5tF4xpnSAhcZ7oLfA | 309 | 358,738 | 152,9 |
| Rondo 1 | https://goo.gl/maps/3CLtGnEQv5ADWbW66 | 306 | 358,775 | 152,6 |
| Varso Tower | https://goo.gl/maps/pPcJMCstWBwEekMC7 | 424 | 358,787 | 152,1 |
| Złota 44 | https://goo.gl/maps/4iWXAWfTY2izz5q67 | 306 | 358,841 | 152,4 |
| Centrum LIM | https://goo.gl/maps/fZWhzx9LNFKasS9u6 | 295 | 358,902 | 152 |
| Pałac Kultury i Nauki | https://goo.gl/maps/xQCPjmHgCvMDv7LG7 | 352 | 358,942 | 152,5 |
| Widok z punktu 50,860768°N, 21,047419°E | ||||
| komin Ciepłowni Kawęczyn | https://goo.gl/maps/s8LuZck61sZdt4JK8 | 392 | 2,028 | 156,6 |
Skąd jednak wiemy, że wyżej wymienione wieże telekomunikacyjne znajdują się właśnie tam? One również zostały sprawdzone w ten sam sposób – na szerszym zdjęciu, gdzie objęły się inne obiekty możliwe do rozpoznania po ich kształcie i położeniu. Po prawej widać Starachowice, których nie sposób pomylić z innym miastem, a po lewej jest charakterystyczny komin dawnej Cementowni Wierzbica (można by było go zidentyfikować np. względem Farmy Wiatrowej Szerzawy znajdującej się bardziej po lewej).
Czy w takim razie nie są to inne obiekty, które znajdują się na azymucie Warszawy, ale bliżej?
Nie ma w tym zakresie azymutów innego skupiska obiektów oznakowanych takimi światłami, które wystawałyby nad horyzontem wyżej niż Warszawa. Teoretycznie gdyby nawet były, to musiałyby być rozmieszczone dokładnie tak samo, jak wieżowce, co byłoby skrajnie mało prawdopodobne.

Świetnie wytłumaczone. Dodam jeszcze, że obliczenia z uśrednionym (ale stałym) współczynnikiem refrakcji nie oddają w pełni warunków tej obserwacji. Obecność warstwy powietrza ze współczynnikiem refrakcji powyżej 1 powoduje, że teoretycznie można zobaczyć wszystko, co wystaje powyżej tej warstwy, dowolnie daleko. Oczywiście w rzeczywistości nie ma tak dobrze, bo po pierwsze, światło ulega rozproszeniu na aerozolach, których zawsze trochę jest, a nawet na cząsteczkach gazów, z których składa się powietrze, a po drugie – warstwa powietrza o tak atrakcyjnych cechach nie jest jednorodna i ma ograniczoną rozciągłość. No, ale wystarczyło i to przez kilka nocy pod koniec maja!
Niestety nie ma lepszego sposobu na oszacowanie refrakcji poprzez obserwację czy analizę zdjęć. Na podstawie tego, jakie obiekty są widoczne nad horyzontem, ewentualnie jak wysoko nad nim wystają, można tylko policzyć średnią wartość tego współczynnika. Różni się ona dla punktów w Warszawie położonych na różnych wysokościach, co świadczy o tym, że obraz został spłaszczony, a refrakcja zmieniała się z wysokością. Nie jest jednak możliwe określenie w ten sposób dokładnego rozkładu współczynnika refrakcji w przestrzeni. Może w przyszłości będzie można zdalnie mierzyć parametry atmosfery w dowolnym miejscu, wtedy dałoby się dokonać takich pomiarów w licznych punktach na linii widzenia – na razie jest to jednak science-fiction. Balonów jest za mało i są za rzadko wypuszczane, by można było szczegółowo określić warunki na linii takiej obserwacji.
Wystarczy wziąć obliczoną zależność współczynnika refrakcji od wysokości, przybliżoną jakąś gładką funkcją i wyznaczyć przebieg linii widzenia. Ja właśnie tak robię – zamiast odtwarzać coś na podstawie zdjęcia, patrzę, co wychodzi z obliczeń i jak ma się to do zdjęcia.
Przybliżenie „wszędzie taki sam pionowy profil współczynnika refrakcji” jest na pewno dokładniejsze od „wszędzie taki sam współczynnik refrakcji, nie zależący od wysokości”, choc oczywiście pozostaje przybliżeniem. Na pewno wychodzi w nim spłaszczenie obrazu.
Inwersja radiacyjna tworzy się nad gruntem położonym na różnej wysokości n.p.m. Przeważająca część terenu pomiędzy Łysą Górą a Warszawą (w tym teren pod odcinkiem linii widzenia biegnącym najniżej n.p.m.) jest usytowana wyżej niż Legionowo od kilkudziesięciu do ponad 100 m, a nieco ponad 100 m nad ziemią inwersja się kończyła. Wobec tego legionowski profil współczynnika refrakcji trzeba by było korygować o ukształtowanie terenu, co skomplikowałoby obliczenia. Bez takiej korekty na długim odcinku linii widzenia pominiemy inwersję, która na tym obszarze najpewniej znajdowała się wyżej niż w Legionowie.
No cóż, trzeba będzie to sprawdzić „w praniu”. Czy wiadomo, jaką wysokość mają maszty w Krogulczy Suchej i w Zabierzowie? Teren w obu miejscach jest na podobnej wysokości, 200 m n.p.m.
Nie wiadomo, na pewno poniżej 100 m.
Pierwszy krok zrobiony. Azymuty potwierdzone, wszystko pod tym względem pasuje, ale dalej nie ruszę bez jakichś wysokościowych punktów odniesienia. Maszty to jedno, a jescze lepsze byłoby coś położonego możliwie blisko. Na prawie tym samym azymucie, co maszt w Zabierzowie, jest jasno świetlony obiekt, znacznie niżej. Wieża kościelna?
Jest wieża kościelna w Starachowicach, ale też o nieznanej wysokości. W kierunku nieco bardziej oddalonym od warszawskich wieżowców jest maszt oraz komin w Radomiu. Ich wysokość jest znana, ale nie zmieściły się w kadrze z centrum Warszawy. Mam je na szerokim ujęciu zrobionym później, kiedy było widać już tylko światło Varso, Pałacu Kultury i komina na Kawęczynie.
Też go namierzyłem. To kościół pod wezwaniem św. Brata Alberta. Wieża na zdjęciach, znalezionych w internecie, wygląda na nie wyższą niż 30 m.
Według modelu NMPT w Geoportalu najwyższy zmierzony punkt wieży tego kościoła ma 271,74 m n.p.m. Ze względu na relatywnie małe zagęszczenie punktów pomiarowych pomiar takich strzelistych obiektów może być jednak obarczony błędem kilku metrów.
Czyli 40 m. Obu masztom też dałem po 40 m, bo to dość częsta wysokość tego typu konstrukcji.
Cały pionowy profil temperatury podniosłem o 50 m – Legionowo leży faktycznie nisko, a nas interesuje raczej teren gdzieś koło Grójca, gdzie linia widzenia najbardziej zbliża się do gruntu. No i coś sensownego powychodziło, ale o tym już kiedy indziej. Północ blisko i idę spać. Dobranoc :-).
Grunt przy kościele jest na ok. 240 m n.p.m. Dla stałego współczynnika refrakcji linia ta na dość długim odcinku biegnie nisko nad gruntem – najbliżej w okolicach Radomia i Białobrzegów. Po uwzględnieniu zmienności refrakcji jej przebieg będzie zapewne nieco inny.
Wydawało mi się, że grunt jest 10 metrów niżej. Coś źle odczytałem. Ale to nic, bo i tak ważny jest czubek wieży, a ten ustawiłem na 270 m n.p.m. Na razie wystawiam tylko wyprodukowany wczoraj opis, naniesiony na zdjęcie „azymuty”:
Link powinien pokazać się w podpisie, w polu „witryna internetowa”.
Napisałem rano komentarz. W polu „witryna internetowa” umieściłem link do wyprodukowanego wczoraj wieczorem opisu, co okazało się krokiem niewłaściwym. Algorytm nie przepuścił i treść albo gdzieś „wisi”, albo została w ogóle usunięta. Bardzo proszę sprawdzić i jeśli jest, to udostępnić.
Gdy będę znowu miał trochę czasu, to zrobię jeszcze obliczenia linii widzenia.
Już jest widoczny, filtr antyspamowy zablokował go ze względu na nietypowy link w tym polu. Varso i Rondo 1 są lekko przesunięte – podejrzewam, że współrzędne wzięte do obliczeń nie odpowiadają najwyższym punktom budynków. Z tym może być problem, nie znalazłem odpowiedniego źródła takich danych. Fotomapy Google i Geoportalu składają się ze zdjęć robionych pod kątem, dlatego górne części budynków są na nich przesunięte względem gruntu. Próbowałem to uwzględnić, ale pewnie pozostały kilkumetrowe różnice.
Dziękuję. Tymi przesunięciami w ogóle bym się nie przejmował. Moim zdaniem mieszczą się w dopuszczalnych granicach błędu.
Współrzędne wziąłem… cóż, poszedłem na łatwiznę i ordynarnie je spisałem z bieżącego artykułu. Z początku trochę mnie zaniepokoiło, że Varso Tower, a zwłaszcza Złota 44, „trafiają” pomiędzy światła, ale potem zobaczyłem, że w Waszych (liczę Pawła Kłaka, stąd liczba mnoga) materiałach podpisy tych dwóch wieżowców też rozciagają się nieco szerzej.
W przyszłości, odnośniki będę raczej umieszczał w treści komentarza – może wtedy algorytm się nie wkurzy.
Wczoraj wieczorem zrobiłem obliczenia i wykresy. Uśredniony współczynnik refrakcji może nadaje się do wyciagnięcia czegoś zza horyzontu, w symulatorze Ulricha, ale poza tym jest zupełnie nierealistyczny!
http://chkw386.ch.pwr.wroc.pl/~strasbur/widoki/LysaGora-Warszawa/widok_Warszawy.html
Dziękuję za obliczenia, rzeczywiście przesunięcie profilu temperatury z Legionowa o 50 m w górę wystarczyło do dobrego dopasowania. Uśredniony współczynnik refrakcji przydaje się do teoretycznego analizowania możliwości obserwacji obiektów. Im większy jest wymagany do widoczności, tym silniej musi zadziałać refrakcja, a obserwacja jest trudniejsza, gdyż rzadziej zdarzają się odpowiednie warunki. Można w ten sposób policzyć również, jak duża część obiektu powinna wystawać nad horyzontem w warunkach zbliżonych do standardowych. Natomiast jeśli chodzi o analizy po wykonanej obserwacji, uwzględnienie danych pomiarowych zdecydowanie lepiej odpowiada rzeczywistości. Potrzebne do tego obliczenia są jednak znacznie bardziej skomplikowane i zwykły arkusz kalkulacyjny tutaj nie wystarczy.
@KrzysiekS Bardzo dobra i trafna analiza na stronie
http://chkw386.ch.pwr.wroc.pl/~strasbur/widoki/LysaGora-Warszawa/widok_Warszawy.html
W pełni zgadzam się z tekstem. Szczególnie istotne jest to zdanie „” światła położone na wysokościach różniących się o około 50 m zdają się leżeć na jednym poziomie. Tylko najwyższy budynek Varso Tower góruje nad nimi, jednak nie tak bardzo, jak wynikałoby z rzeczywistej przewagi wysokości””
Ten sam efekt „spłaszczenia” widać było na zdjęciach masztu w Raszynie – widoczne jest chyba 5 świateł które w rzeczywistości dzieli około kilkadziesiąt metrów a na zdjęciu zostały „spłaszczone” , tak , że po obliczeniu rozmiaru kątowego widocznej części masztu na zdjęciu – maszt „skurczył się” wskutek „zanurzenia się” w warstwie inwersyjnej.
Podobne przemyślenia mieliśmy po obserwacji oraz po analizie „uśrednionego współczynnika” refrakcji dla Varso oraz PKiN.
Wartość dla tych obiektów znacznie się różniła (bodajże 0,4 i 0,44) , przeliczenie rozmiarów kątowych widocznych obiektów i porównanie z rzeczywistymi
różnicami w wysokości budynków sugerowało że Varso jest „spłaszczone”.
Ta warstwa inwersyjna „pływała” co widać np, na GIFie umieszczonym na dalekiewidoki.pl .
O ile wystąpienie samej inwersji można przewidzieć np. wykorzystując narzędzia radiosondaży w aplikacji WIndy , tak praktycznie niemożliwym jest przewidzenie „skali” , „grubości” i intensywności tej inwersji na konkretnym obszarze lub w konkretnym punkcie.
Oczywistym jest , że refrakcja jest zmienna w czasie na różnej wysokości i nie można jej zamknąć w uśrednionym współczynniku.
Uśredniony współczynnik refrakcji nie oddaje dynamiki refrakcji na całej linii widzenia.
Natomiast mimo jego „niedoskonałości” i nie mając innych narzędzi jest pomocny np. w teoretycznym analizowaniu możliwości obserwacji.
Idealnie byłoby stworzenie programu ,w którym wskazujesz plik z danymi z sondażu, współrzędne początku i końca linii obserwacji, zdjęcie i dostajesz wynik.
Zapewne większość z tych fukcjonalności robi Twój program , ale obawiam się , że poza Tobą nikt go jeszcze nie rozgryzł 🙂 Może jakiś update na nowsze systemy? – ubuntu, win10 ? 🙂
Pozdrawiam serdecznie.