Spis treści
- Wstęp
- Obliczenia dla płaskiej planety
- Obliczenia dla kulistej Ziemi
- Wpływ refrakcji atmosferycznej
- Wpływ zmienności refrakcji atmosferycznej
Wstęp
Zdjęcia na duże odległości, zwłaszcza Tatry widziane z daleka, wywołują liczne komentarze na temat kształtu naszej planety, a także dyskusje czy taki widok jest możliwy.
Prawda jest taka, że obserwacje potwierdzają obecność i wielkość krzywizny Ziemi, a także występowanie zjawiska refrakcji światła w atmosferze. Widać taką część odległych gór (czy też innych obiektów), jaka powinna być widoczna przy uwzględnieniu tych czynników i ukształtowania terenu na linii obserwacji. Dalekie widoki na płaskiej planecie wyglądałyby zupełnie inaczej – oddalone pasma górskie byłyby widoczne w całości, a nie tylko partie szczytowe.
Najlepiej przeanalizować to na przykładzie. Dobrze nadaje się do tego zdjęcie przedstawiającego odległe góry – widok na Bieszczady z Radziejowej w Beskidzie Sądeckim.
Zdjęcie zostało zrobione z wysokości ok. 1284 m n.p.m. Przed Bieszczadami widać górę z charakterystycznym masztem – to Stebnicka Magura na Słowacji (900 m n.p.m.), oddalona o 47,4 km. Tuż poniżej jej szczytu (na wys. 896 m n.p.m.) stoi maszt o wysokości 81 m. Za nią, po prawej stronie widnieje Roh (1255 m n.p.m.) – najwyższy wierzchołek Połoniny Wetlińskiej, do którego odległość wynosi 142,9 km. Jego szczyt jest widoczny minimalnie poniżej poziomu masztu. No właśnie – poniżej, a Roh jest prawie 300 metrów wyżej niż szczyt masztu. Na płaskiej planecie byłoby to niemożliwe, bieszczadzkie wierzchołki musiałyby wystawać znacznie wyżej.
Obliczmy więc kąt, pod którym widać te obiekty względem płaszczyzny poziomej dla Radziejowej (oznaczmy go literą α). Im większy jest ten kąt, tym obiekt jest widoczny wyżej. Wykorzystamy tu fakt, że dla małych kątów sinus jest w przybliżeniu równy wielkości kąta wyrażonej w radianach – dla 1° błąd wynosi zaledwie 0,005%, dla mniejszych kątów jeszcze mniej, więc dokładność tak uproszczonych obliczeń pozostaje bardzo duża.
Do obliczeń niezbędne będą następujące dane:
- wysokość punktu obserwacji (taras wieży widokowej na Radziejowej): 1284 m n.p.m.
- wysokość masztu na Stebnickiej Magurze: 977 m n.p.m.
- wysokość Roha: 1255 m n.p.m.
- odległość Radziejowa – maszt: 47,4 km = 47400 m
- odległość Radziejowa – Roh: 142,9 km = 142900 m
Obliczenia dla płaskiej planety
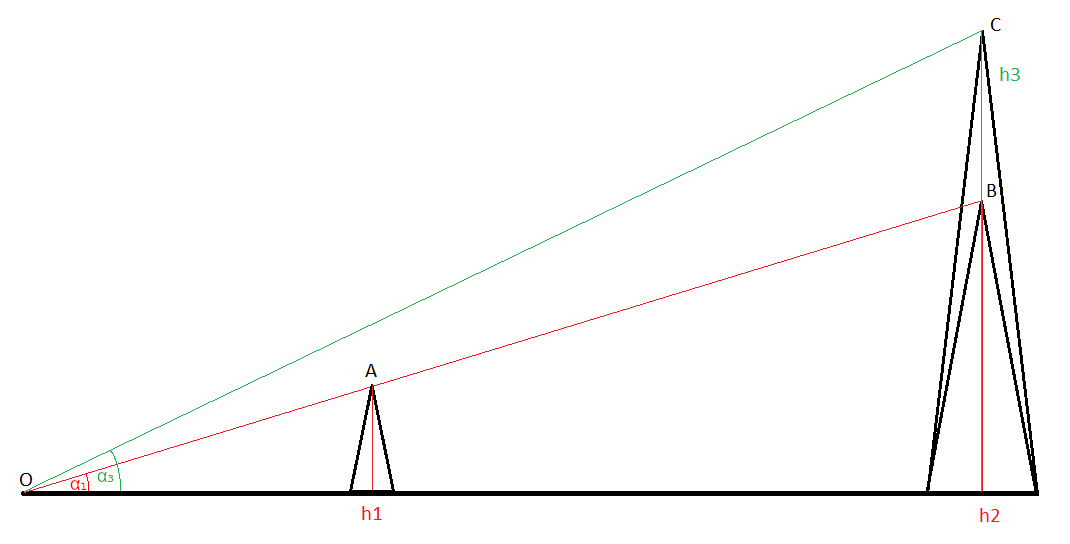
Na płaskiej planecie sinus kąta α (a więc w wystarczająco dokładnym przybliżeniu miara tego kąta) jest ilorazem różnicy wysokości pomiędzy widzianym obiektem a punktem, z którego prowadzimy obserwację oraz odległości.
Liczymy więc kąt dla masztu:
α = (977 – 1284) / 47400 ≈ -0,00648 rad = -22’16,6″
oraz dla Roha:
α = (1255 – 1284) / 142900 ≈ -0,00020 rad = -0’41,9″
Minus oznacza widoczność poniżej płaszczyzny poziomej. Maszt powinien być więc widoczny ponad 21 minut kątowych poniżej Roha, gdyż tyle wynosi różnica pomiędzy obliczonymi kątami. Możemy porównać to z wysokością masztu. Z definicji łukowej miary kąta wynika, że owa różnica kątów (w radianach) pomnożona przez odległość do Magury da nam wysokość nad jej szczytem, na poziomie której powinien być widoczny Roh. Liczymy więc: (-0,0002 – (-0,00648)) * 47400 m ≈ 298 m – oznacza to, że na płaskiej Ziemi Roh powinien być widoczny na poziomie punktu położonego 298 metrów powyżej szczytu masztu. Widoczność Roha poniżej masztu jest dowodem na wypukłe zakrzywienie Ziemi.
Na tym można by było poprzestać, ale sprawdźmy czy krzywizna Ziemi ma odpowiednią wielkość.
Obliczenia dla kulistej Ziemi
Przyjmijmy kulisty kształt Ziemi o promieniu 6371 km.
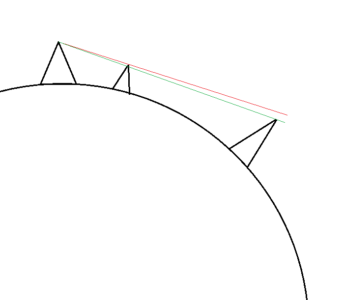
Na kąt, pod jakim widać obiekt, wpływa zakrzywienie planety. Im większa odległość, tym większe zakrzywienie – odległy teren coraz bardziej „ucieka” w dół. Jest więc możliwe, że wyższy obiekt, ale położony dalej, będzie widoczny poniżej niższego, położonego bliżej, nawet jeśli punkty te są położone niżej niż miejsce prowadzenia obserwacji.
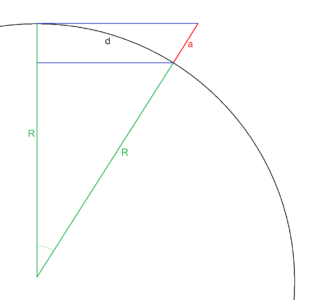
Wielkość pozornego zmniejszenia wysokości, czyli dokładniej odległość pomiędzy płaszczyzną prostopadłą do pionu w danym punkcie a punktem znajdującym się na tej samej wysokości n.p.m. (nazywaną płaszczyzną horyzontu astronomicznego), położonym w odległości d mierzonej wzdłuż obwodu planety (jako długość łuku), można obliczyć następującym wzorem: a = R (1 / cos (d / R) – 1), gdzie R – promień Ziemi.
Wyprowadzenie wzoru na podstawie poniższego rysunku.
z definicji funkcji cosinus: cos (d / R) = R / (R + a)
(R + a) * cos (d / R) = R
a = R + a = R / cos (d / R)
a = R / cos (d / R) – R
a = R (1 / cos (d / R) – 1)
Dla masztu na Stebnickiej Magurze:
a = 6371 km * (1 / cos (47,4 km / 6371 km) – 1) ≈ 0,176 km = 176 m
Dla Roha:
a = 6371 km * (1 / cos (142,9 km / 6371 km) – 1) ≈ 1,603 km = 1603 m
Kąty α wynoszą zatem:
dla masztu α = (977 – 176 – 1284) / 47400 ≈ -0,01019 rad = -35’1,8″
dla Roha α = (1255 – 1603 – 1284) / 142900 ≈ -0,01142 rad = -39’15,7″
Roh powinien być widoczny 4’13,9″ poniżej wierzchołka masztu, czyli mniej więcej na poziomie 1/4 wysokości masztu. Na zdjęciu Roh jest jednak wyżej, prawie na poziomie szczytu masztu. Z czego może to wynikać?
Wpływ refrakcji atmosferycznej
Zjawisko to nosi nazwę refrakcji atmosferycznej. Zależy ona głównie od ciśnienia atmosferycznego, temperatury i wielkości pionowego gradientu termicznego, czyli zmiany temperatury powietrza z wysokością. Jej miarą jest współczynnik refrakcji, definiowany jako stosunek promienia krzywizny Ziemi do promienia krzywizny toru światła. Można go obliczyć ze wzoru k = 503 * p / T² * (0,0342 + dT / dh), gdzie p – ciśnienie w hPa, T – temperatura w kelwinach, dT / dh – pionowy gradient temperatury na 1 m wysokości. Przyjmuje się, że w standardowych warunkach k = 0,13, jednak przy niestandardowym rozkładzie temperatury, np. przy inwersji temperatury, wartość k może być wyższa, lokalnie nawet powyżej 1.
Matematyczne i fizyczne podstawy tego zjawiska wraz z wyprowadzeniem wzorów przedstawił na swojej stronie Walter Bislin.
Dla masztu na Stebnickiej Magurze:
a = 7323 km * (1 / cos (47,4 km / 7323 km) – 1) ≈ 0,153 km, α = (977 – 153 – 1284) / 47400 ≈ -0,00970 rad
Dla szczytu Roha:
a = 7323 km * (1 / cos (142,9 km / 7323 km) – 1) ≈ 1,394 km, α = (1255 – 1394 – 1284) / 142900 ≈ -0,00996 rad
Różnica kątów pomnożona przez odległość do masztu jest równa (0,00996 – 0,0097) * 47400 m = 12,3 m. Dla refrakcji o współczynniku 0,13 Roh powinien być widoczny na poziomie punktu znajdującego się 12 m poniżej szczytu masztu. Wartość ta jest zbliżona do tego, co widzimy na zdjęciu. Dalekie widoki są więc dowodem nie tylko na kulistość Ziemi, ale również na zjawisko refrakcji atmosferycznej.
Tak naprawdę Ziemia nie jest kulą, lecz geoidą – bryłą zbliżoną do elipsoidy obrotowej, spłaszczoną na biegunach ze względu na siłę odśrodkową wynikającą z ruchu obrotowego. Różnica względem kształtu kulistego jest jednak na tyle mała, że nie wpływa w sposób zauważalny na obserwowany widok.
- p = 1000 hPa, T = 298 K (25 °C), dT/dh = -0,007 K/m, h = 0,3 km
- p = 1000 hPa, T = 263 K (-10 °C), dT/dh = 0,01 K/m (inwersja temperatury – wzrost o 1 K na 100 m wysokości), h = 0,3 km
W pierwszym przypadku:
k = 503 * 1000 / 298² * (0,0343 + (-0,007)) ≈ 0,1546
r = 6371 km / (1 – 0,1546) ≈ 7536 km
d = (0,3 km * (2 * 7536 km + 0,3 km))0,5 ≈ 67,25 km
W drugim przypadku:
k = 503 * 1000 / 263² * (0,0343 + (0,01)) ≈ 0,3222
r = 6371 km / (1 – 0,3222) ≈ 9399 km
d = (0,3 km * (2 * 9399 km + 0,3 km))0,5 ≈ 75,1 km
Zmiana temperatury z 25 °C na -10 °C oraz wystąpienie inwersji termicznej zwiększyły zasięg widoczności o ok. 12%. Obliczenia dotyczą jednak obserwatora znajdującego się nad terenem równinnym – w rzeczywistości zmiana zasięgu widoczności bywa inna i zależy od ukształtowania terenu, a także od zmienności refrakcji atmosferycznej w przestrzeni – przede wszystkim w zależności od wysokości. Wzór na współczynnik refrakcji dotyczy bowiem warunków lokalnych – w określonym miejscu.
Wpływ zmienności refrakcji atmosferycznej
W nocy, w warunkach inwersji radiacyjnej, obserwowano obiekty, dla widoczności których minimalny średni współczynnik refrakcji wynosi ok. 0,5 (np. światła wieżowców w Warszawie z Łysej Góry w Górach Świętokrzyskich).
Nawet pomimo tak silnej refrakcji wpływ krzywizny Ziemi na widziany krajobraz jest wyraźnie widoczny.