Widok na góry z dużej odległości wyraźnie różni się od panoram z bliska. Różnice te bywają źródłem złudzeń, którym ulegają czasem także osoby dobrze zaznajomione z topografią widocznego pasma górskiego. Pod zdjęciami Tatr z Wyżyny Lubelskiej można trafić na komentarze, pisane również przez osoby zawodowo związane z Tatrami, w których podważana jest prawidłowość oznaczeń szczytów – są one rzekomo oddalone za daleko od siebie, powinny być zupełnie inaczej rozmieszczone czy też nie powinny być możliwe do rozróżnienia ze względu na dużą odległość. Specyfika widoków z daleka sprawia więc, że pomimo szczegółowej znajomości topografii, bez zrozumienia geometrii przestrzennej i zjawisk zachodzących w atmosferze można ulec pewnym złudzeniom i stereotypom.
- Za sprawą ukształtowania terenu i krzywizny Ziemi podnóże gór jest zasłonięte przez bliżej położone tereny. Im niżej linia obserwacji przebiega nad znajdującym się po drodze terenem, tym widać mniejszą część szczytów. Dlatego widok ze szczytu znacznie górującego nad otoczeniem różni się od widoku z tej samej odległości z niewielkiego wzgórza. Przykładem są Tatry widziane z Pradziada w czeskich Sudetach oraz z podobnej odległości z kamieniołomu w Łysakowie na skraju Wyżyny Lubelskiej.
Tatry Wysokie z Pradziada (max. odległość 236,6 km) – fot. Tobiasz Rangno Tatry Wysokie z Łysakowa (max. 230,5 km) Wysokość Pradziada to 1491 m n.p.m., natomiast szczyt kamieniołomu w Łysakowie znajduje się na 250 m n.p.m. Pomiędzy Pradziadem a Karpatami nie ma większych wzniesień, linia obserwacji przebiega wysoko nad ziemią, więc tatrzańskie szczyty wystają dość wysoko. Z Łysakowa widoczne są zaledwie wierzchołki najwyższych szczytów, ponieważ resztę zasłaniają tereny położone na linii obserwacji, znajdujące się niewiele niżej niż punkt widokowy. Taki widok może powodować błędne wnioski dotyczące wzajemnego położenia szczytów – sąsiednie szczyty mogą wydawać się odsunięte zbyt daleko od siebie. Złudzenie to polega na tym, że odległość między nimi porównujemy z wysokością ich widocznych części, która jest wielokrotnie mniejsza od wysokości tych szczytów względem podnóża.
Patrząc na Tatry z sąsiednich pasm górskich, widzimy potężne szczyty wznoszące się ponad kilometr nad okolicę. Sąsiednie szczyty wydają się być blisko siebie, ponieważ widoczne odstępy między nimi są niewielkie w porównaniu z ich wysokością. Inaczej jest jednak, jeśli widać tylko same wierzchołki – zamiast majestatycznych zboczy, nad horyzontem wystają tylko szczytowe partie gór, zaledwie kilkanaście lub kilkadziesiąt metrów. Obserwowane odstępy pomiędzy szczytami są analogiczne jak w przypadku obserwacji z mniejszej odległości i tego samego kierunku, ale w porównaniu z kilkanaście czy kilkadziesiąt razy mniejszą wysokością widocznych części zboczy mogą wydawać się duże.
Porównanie zdjęcia Tatr z Łysakowa z symulacją widoku z wysokości 1000 m nad ziemią, gdzie widoczna jest dużo większa część szczytów. Pokazuje ono, jak duża część gór jest schowana za horyzontem. - Podobnie jak w przypadku krajobrazów oglądanych z bliska, widoczne odstępy między szczytami nie odpowiadają bezpośrednio odległościom pomiędzy nimi. Zależą one także od wzajemnego usytuowania szczytów względem kierunku obserwacji – dokładnie od różnicy azymutów pomiędzy kierunkiem obserwacji a linią łączącą wierzchołki. Jeśli wynosi ona 0°, szczyty są widoczne w jednej linii jeden za drugim, natomiast przy 90° są one oddalone od miejsca obserwacji o taką samą odległość i tylko wtedy widzimy pełną długość odcinka między nimi. Dla małych różnic azymutów pomiędzy widocznymi szczytami i małych różnic odległości pomiędzy nimi w porównaniu z odległością od punktu obserwacji można zastosować przybliżony wzór:
,
w którym a’ – pozorna, obserwowana długość odcinka pomiędzy szczytami, a – rzeczywista odległość między szczytami, α1 – azymut od punktu obserwacji do widocznego szczytu (wzór jest dla małej różnicy azymutów, więc nie ma istotnego znaczenia, do którego szczytu podamy azymut), α2 – azymut linii łączącej szczyty.
a’ jest to długość rzutu odcinka pomiędzy szczytami na płaszczyznę prostopadłą do kierunku obserwacji, oddaloną od miejsca obserwacji o odległość równą w przybliżeniu średniej odległości do widocznych szczytów.
Pozorna, obserwowana długość odcinka między szczytami a’ jest mniejsza od rzeczywistej długości odcinka a, jeśli odcinek ten nie jest prostopadły do kierunku obserwacji. Na zdjęciu Tatr z Łysakowa widzimy, że Gerlach wydaje się być bliżej Lodowego Szczytu niż Baranie Rogi. W rzeczywistości jednak odległość od Lodowego do Baranich Rogów wynosi ok. 1,1 km, a do Gerlacha ok. 5,2 km. Gerlach jest jednak położony o ok. 5,2 km dalej, więc odcinek Lodowy-Gerlach przebiega pod małym kątem w stosunku do kierunku obserwacji.
Wątpliwości rozwiewa nałożenie na zdjęcie mapy z narysowanymi liniami od punktu w Łysakowie do widocznych szczytów.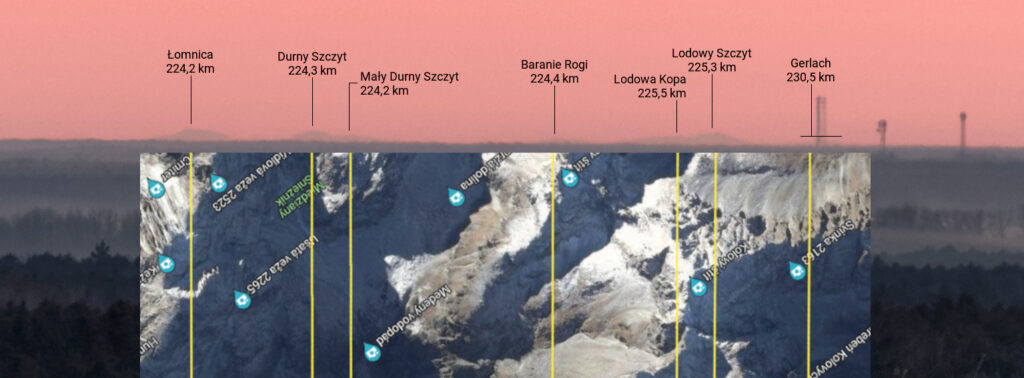
Zdjęcie Tatr z Łysakowa z nałożonym fragmentem mapy Google, na której żółte linie przebiegają od Łysakowa do widocznych szczytów Ponadto widoczny układ szczytów (ich wzajemne usytuowanie na panoramie) zależy od kierunku, z jakiego są obserwowane z uwagi na paralaksę.
Często zdarzają się też komentarze odwołujące się do obliczeń geometrycznego zasięgu widoczności, według których takie widoki miałyby być niemożliwe ze względu na krzywiznę Ziemi. Najprostszy wzór na ów zasięg jest następujący: d = 3,57(√h1+√h2), gdzie h1, h2 to wysokości punktu, z którego jest prowadzona obserwacja i punktu obserwowanego. Wzór ten jest prawidłowy (zawiera niewielkie uproszczenie) i wynika z twierdzenia Pitagorasa. Nie uwzględnia jednak ukształtowania terenu ani załamania światła w atmosferze, dlatego jeśli wstawimy w nim wysokości n.p.m., to poprawny wynik otrzymamy wyłącznie dla morza lub równiny na poziomie morza, na planecie, na której nie ma atmosfery.
Punkty widokowe znajdują się na ogół na wzniesieniach, a zatem teren na linii widzenia obniża się poniżej ich wysokości, odsłaniając widok. Dlatego w obliczeniach wspomnianym wzorem należałoby podawać wysokości względem punktu, w którym promienie światła od widzianego obiektu do obserwatora biegną najniżej nad poziomem terenu. Można go wyznaczyć m.in. za pomocą narzędzia online Heywhatsthat. Co więcej, istotną rolę odgrywa załamanie światła w powietrzu (refrakcja atmosferyczna), dzięki któremu widać obiekty nieco wyżej niż miałoby to miejsce, gdyby Ziemię otaczała próżnia. Zjawisko to (w jego standardowej wielkości) można uwzględnić we wzorze, zwiększając współczynnik z 3,57 do 3,83. - Pozorne zmniejszenie wysokości bardziej odległych szczytów względem bliższych. Jest wywołane przez krzywiznę Ziemi. Im dalej, tym powierzchnia Ziemi coraz bardziej odchyla się w dół względem płaszczyzny poziomej dla miejsca obserwacji, dlatego wyższe szczyty położone dalej mogą być widoczne niżej w stosunku do bliżej zlokalizowanych, niższych wierzchołków. Gerlach widziany z Łysakowa wydaje się niższy od Lodowego Szczytu, mimo że w rzeczywistości jest wyższy. Znajduje się jednak o ponad 5 km dalej, więc bardziej „chowa się” za krzywizną Ziemi.
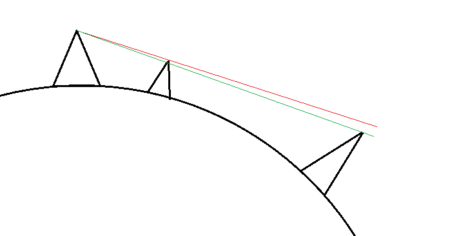
Pozorne obniżenie dalej położonego obiektu spowodowane krzywizną Ziemi - Wpływ niejednorodnego załamania światła w atmosferze. Światło, pokonując duży dystans w powietrzu o zróżnicowanej temperaturze z obecnością turbulencji, ulega nieregularnemu załamaniu, co powoduje pogorszenie ostrości obrazu. Dlatego też z reguły nie jest możliwe dostrzeżenie z bardzo daleka niewielkich turni położonych blisko siebie czy budynków znajdujących się na szczytach, mimo posługiwania się sprzętem teoretycznie pozwalającym na ich obserwację. Zjawisko to może mieć różne nasilenie, jednak przeważnie nie jest aż tak intensywne, by nie dało się rozróżnić większości szczytów widocznych z danego miejsca.
- Z załamaniem światła związane jest jeszcze jedno zjawisko – refrakcja atmosferyczna. Jest to zakrzywienie promieni świetlnych przebiegających w atmosferze spowodowane zmianami gęstości powietrza z wysokością. Występuje ona prawie zawsze, z wyjątkiem bardzo dużego pionowego gradientu temperatury, ponadto nie dotyczy promieni świetlnych biegnących pionowo – tych jednak nie wykorzystujemy przy obserwacjach naziemnych. Nasilenie tego zjawiska ulega niekiedy zwiększeniu, wtedy nad horyzontem mogą pojawić się obiekty zazwyczaj niewidoczne. Jeśli zwiększona refrakcja występuje w stosunkowo cienkiej warstwie powietrza, promienie świetlne biegnące od różnych szczytów i punktów na ich zboczach mogą przebywać w niej inny dystans. Te, które pokonują w niej większą drogę, ulegają silniejszemu zakrzywieniu. W rezultacie często obserwujemy pozorne spłaszczenie kształtu szczytów – wierzchołek jest słabiej podniesiony nad horyzont w stosunku do zboczy. Ponadto w tym przypadku silniejszy jest wpływ refrakcji na niższe, a także odleglejsze szczyty – dlatego na zdjęciu z Łysakowa Gerlach wystaje wyżej względem komputerowej symulacji w porównaniu z pozostałymi szczytami. W skrajnych przypadkach, gdy występuje silna inwersja temperatury, strzeliste szczyty przybierają kształt łagodnych wzniesień lub nawet poziomych linii.
Spłaszczony w wyniku inwersji temperatury obraz Tatr widzianych z Łychowa Gościeradowskiego (woj. lubelskie) Widok ze Śnieżnika – odległe o niemal 300 km alpejskie szczyty wyglądają jak prawie poziome linie wystające nad warstwę inwersji (fot. i opis – Krzysztof Strasburger) - Jak w przypadku każdego obiektu, na który patrzymy – im większa odległość dzieli nas od niego, tym zajmuje on mniejszą część pola widzenia oka. Góry widziane z daleka wydają się mniejsze – mają mniejsze rozmiary kątowe, dlatego do tego typu obserwacji używa się teleobiektywów i lornetek powiększających obraz.




