Spis treści
- Czym jest refrakcja atmosferyczna?
- Od czego zależy wielkość refrakcji?
- Wpływ refrakcji na dalekie widoki
- Refrakcja a zasięg widoczności
- Refrakcja w symulacjach widoczności
Czym jest refrakcja atmosferyczna?
Jest to załamanie światła w powietrzu wynikające ze zmian gęstości atmosfery z wysokością. Te z kolei są spowodowane przede wszystkim zmianami ciśnienia atmosferycznego i temperatury powietrza.
Światło w atmosferze Ziemi zazwyczaj nie biegnie po linii prostej – tak byłoby w próżni. Zgodnie z prawem Snelliusa kierunek biegu promienia światła ulega zmianie na granicy ośrodków o różnych współczynnikach załamania. Jest to dokładnie to samo zjawisko, które obserwujemy na granicy powietrza i wody albo powietrza i szkła, np. w soczewkach. Tutaj nie ma jednak ostrej granicy między ośrodkami – zmiany właściwości powietrza są płynne, dlatego zamiast gwałtownej zmiany kierunku promienia światła mamy stopniowe, łagodne zakrzywienie na dużym dystansie.
Refrakcja atmosferyczna występuje zawsze, z dwoma wyjątkami – obserwacji w pionie (światło nie ulega załamaniu, gdy pada prostopadle do powierzchni granicznej między ośrodkami) oraz przy silnie zwiększonym pionowym gradiencie termicznym, np. nad zbiornikiem wodnym cieplejszym od powietrza. W tym drugim przypadku spadek gęstości atmosfery związany ze zmianami ciśnienia jest równoważony przez wzrost gęstości z powodu obniżania temperatury.
Jej miarą jest współczynnik refrakcji, definiowany jako stosunek promienia krzywizny Ziemi do promienia krzywizny toru światła. Jego lokalna wartość jest określona następującym wzorem:
gdzie p – ciśnienie atmosferyczne w hPa, T – temperatura powietrza w kelwinach, dT / dh – pionowy gradient temperatury na 1 m różnicy wysokości (w K/m). Można ją obliczyć za pomocą arkusza kalkulacyjnego. Jego wyprowadzenie znajdziemy np. na tej stronie. Jest to uproszczony wzór, nieuwzględniający czynników wpływających na refrakcję w małym stopniu, takich jak wilgotność powietrza.
Od czego zależy wielkość refrakcji?
Największy wpływ na wartość współczynnika refrakcji ma pionowy gradient temperatury, czyli tempo zmiany temperatury powietrza z wysokością. Standardowo wynika on z przemiany adiabatycznej zachodzącej przy sprężaniu i rozprężaniu powietrza, które towarzyszą zmianom wysokości (im wyżej, tym ciśnienie atmosferyczne jest niższe) i wynosi ok. -0,65 °C/100 m, jeśli podczas wznoszenia powietrza zachodzi skraplanie pary wodnej oraz ok. -1 °C/100 m w suchym powietrzu, gdy kondensacja pary nie występuje. Rozkład temperatury w zależności od wysokości może jednak ulegać zmianie, na przykład podczas inwersji temperatury, gdy ze wzrostem wysokości powietrze staje się cieplejsze. Wówczas gradient może sięgać kilkunastu stopni na 100 m, jego wartość liczbowa jest wtedy dodatnia (w warunkach standardowych jest ujemna). W dalekich obserwacjach spotykamy się z kilkoma typami inwersji.
- Inwersja osiadania – występuje w wyżu barycznym, w wyniku zstępujących ruchów powietrza, które ogrzewa się adiabatycznie, stając się cieplejsze od warstwy powietrza znajdującego się niżej. Mamy z nią do czynienia w górach i czasem na pogórzach, podczas wyżowej pogody, zwłaszcza zimą. Opadające ku dołowi powietrze jest bardzo suche, czyste i o wyjątkowo dobrej widzialności, jednak warstwa leżąca poniżej charakteryzuje się obniżoną przejrzystością, z dużą koncentracją zanieczyszczeń i nierzadko wilgoci. Dlatego na obszarze oddziaływania silnego wyżu na małych wysokościach często trudno o dalekie widoki, podczas gdy kilkaset metrów wyżej widzialność może sięgać setek kilometrów.
- Inwersja radiacyjna – powstaje poprzez wypromieniowanie ciepła z gruntu podczas bezchmurnej i bezwietrznej pogody pod koniec dnia oraz w nocy. Przygruntowa warstwa powietrza ochładza się szybciej niż powietrze znajdujące się wyżej. Ten rodzaj inwersji w szczególnym stopniu wpływa na obserwacje w regionach o małym urozmaiceniu ukształtowania terenu, gdzie linia widzenia na długim odcinku przebiega nisko nad gruntem.
- Inwersja adwekcyjna – pojawia się przy napływie cieplejszego powietrza nad chłodniejsze podłoże. Podobnie jak inwersja radiacyjna dotyczy przygruntowej warstwy powietrza. Może występować nad zbiornikami wodnymi.
Istotne znaczenie ma sama wartość temperatury powietrza – w chłodniejszym powietrzu refrakcja jest silniejsza.
Wpływ ciśnienia atmosferycznego na zmienność refrakcji w danym miejscu jest stosunkowo niewielki – zmiany ciśnienia na stałej wysokości n.p.m. nie są duże. Jest jednak ważnym czynnikiem, jeśli rozpatrujemy refrakcję na dużych wysokościach – ze wzrostem wysokości maleje ciśnienie, zmniejsza się więc współczynnik refrakcji.
Wilgotność powietrza wpływa w zauważalny sposób na refrakcję, jeśli silnie zmienia się z wysokością – np. nad wodą.
Wstawiając do ww. wzoru typowe wartości spotykane w polskim klimacie, otrzymujemy wartości wyższe od uznawanych za średnie 0,13-0,14. Przy pionowym gradiencie temperatury -1 °C/100 m (wartość typowa dla suchego powietrza) i ciśnieniu 1013 hPa wartość 0,13 występuje dopiero przy temperaturze 35 °C. Z obliczeń tych wynika, że zazwyczaj w polskim klimacie mamy do czynienia z nieco większymi wartościami w okolicach 0,15-0,17.
Przykładowe wartości dla różnych warunków (minus przy gradiencie termicznym oznacza spadek temperatury ze wzrostem wysokości):
| temperatura [°C] | gradient temperatury w °C na 100 m | ciśnienie [hPa] | współczynnik refrakcji |
| 20 | -0,65 | 1000 | 0,163 |
| -10 | -0,65 | 1000 | 0,202 |
| 20 | -0,65 | 900 | 0,146 |
| 20 | -1 | 1000 | 0,142 |
| 20 | 1 | 1000 | 0,26 |
| 0 | 2 | 1000 | 0,366 |
| 30 | -2 | 1000 | 0,078 |
Wpływ refrakcji na dalekie widoki
Refrakcja atmosferyczna powoduje zwiększenie zasięgu widoczności i umożliwia obserwację obiektów, które przy jej braku byłyby schowane za horyzontem. Im jest silniejsza, tym odległe obiekty coraz bardziej wystają nad horyzontem. Jej znaczenie w dalekich obserwacjach dotyczy przede wszystkim widoczności obiektów z odległości bliskich maksymalnym – dzięki zwiększonej refrakcji możliwe są obserwacje z miejsc położonych dalej niż w warunkach standardowych.

W wyniku refrakcji obserwowany obiekt jest widoczny wyżej niż gdyby światło przebiegało w linii prostej. Wielkość tego pozornego zwiększenia wysokości jest określona następującym wzorem, w którym h – wysokość pozornego podniesienia, d – odległość, k – współczynnik refrakcji, R – promień Ziemi:
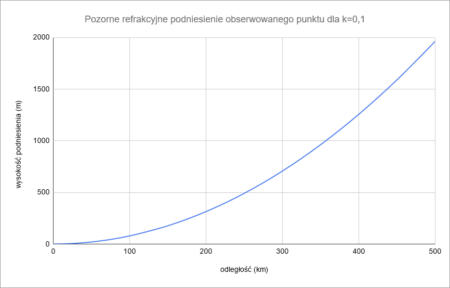
Podniesieniu ulega cały widoczny krajobraz, dlatego aby określić jego wartość względem bliżej położonego punktu, należy od podniesienia punktu dalszego odjąć podniesienie punktu bliższego pomnożone przez iloraz odległości do punktu dalszego i bliższego:
Powyższe wzory zawierają przybliżenia dla małych kątów – są jednak wystarczająco dokładne dla odległości, na które możliwe są obserwacje z Ziemi.
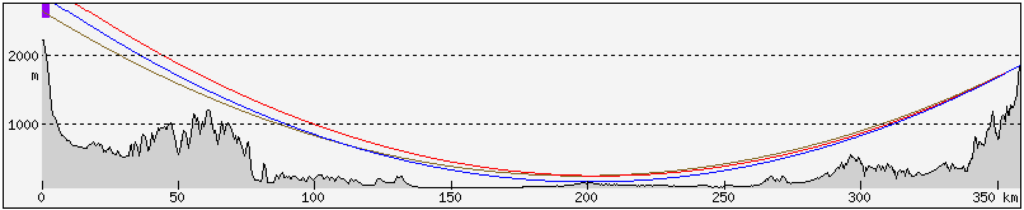
Programy wyznaczające zasięg widoczności i symulujące panoramy widokowe uwzględniają w obliczeniach współczynnik refrakcji 0,13. Jak widać w powyższej tabeli, osiąga on ok. 0,14 przy gradiencie -1 °C / 100 m w temperaturze 20 °C, czyli w typowych warunkach w suchym powietrzu w ciepłej połowie roku. Przez większą część roku mamy w Polsce niższe temperatury, jesienią czy zimą częsty jest więc wzrost tego parametru w okolice 0,17-0,2 w dolnej części troposfery. Tatry z największych odległości w Polsce, czyli z Wyżyny Lubelskiej i Roztocza najlepiej obserwować jesienią i zimą ze względu na korzystny azymut zachodzącego słońca, a co za tym idzie – podświetlenie nieba o zmierzchu, zwiększające kontrast. Nie jest więc niczym dziwnym, że często widać je z wielu miejsc nieuwzględnianych przez symulacje. Teoretycznie najlepsze warunki refrakcyjne powinny być przy silnym mrozie i bezchmurnym niebie, jednak w Polsce na terenach nizinnych i wyżynnych przeważnie jest wtedy duże zanieczyszczenie powietrza, znacznie ograniczające widzialność.
Obserwacje Tatr z Wyżyny Lubelskiej pokazują, że w chłodniejszej połowie roku po zachodzie słońca współczynnik refrakcji często osiąga wartości 0,2-0,22. Jest to wartość uśredniona, obliczona na podstawie zdjęć. Obserwacje w takich regionach charakteryzują się przebiegiem światła na długim dystansie na niewielkiej wysokości nad poziomem terenu, gdzie może występować inwersja radiacyjna. Ze zdjęć wynika, że na tym obszarze wartość bywa jeszcze wyższa (okolice 0,3 nad lasami Kotliny Sandomierskiej), natomiast dalej i wyżej – wyraźnie niższa, dając w rezultacie podobny efekt, jakby na całym dystansie był stały współczynnik refrakcji nieco powyżej 0,2.

W górach w warunkach inwersji osiadania obserwowano szczyty, dla widoczności których minimalny średni współczynnik refrakcji wynosi ok. 0,3 (np. Heukuppe w austriackich Alpach ze Śnieżnika).

Inwersja radiacyjna występuje w dość cienkiej warstwie powietrza nad gruntem. Z tego względu obserwacje niżej położonych obiektów mogą charakteryzować się znacznie silniejszym wpływem refrakcji niż obserwacje wysokich gór, w przypadku których światło pokonuje dużą część dystansu powyżej inwersji. Z Kalenic niedaleko Łowicza zostały sfotografowane światła warszawskich wieżowców, z których najniższe powinny być widoczne przy stałym współczynniku refrakcji ok. 0,5. Pomiary sondażowe temperatury powietrza pokazują, że lokalnie współczynnik ten może osiągać wartość powyżej 1 (analiza przykładowego pomiaru z Legionowa w poście Warszawa widziana z Kalenic).

W przypadku obserwacji z odległości bliskich maksymalnym, gdy w standardowych warunkach obiekt jest schowany tuż poniżej horyzontu, można obliczyć współczynnik refrakcji umożliwiający widoczność (przy założeniu jego stałej wartości). Można w tym celu wykorzystać arkusz kalkulacyjny, posługując się opisaną tu metodą. Możliwe jest też obliczenie pozornego podniesienia horyzontu pod wpływem refrakcji za pomocą tego arkusza.
Niejednorodność refrakcji może powodować zniekształcenie obrazu. W skrajnych przypadkach widoczne są duże deformacje o charakterze mirażu – dotyczy to znacznych zmian refrakcji w cienkiej warstwie powietrza, które czasem towarzyszą obserwacjom w warunkach inwersji osiadania.
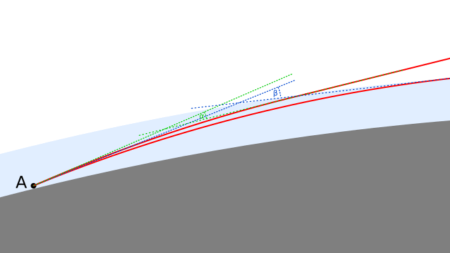
Może też wystąpić spłaszczenie obrazu – często, w różnym stopniu towarzyszy obserwacjom Tatr z Wyżyny Lubelskiej, gdzie światło na długim odcinku biegnie nisko nad ziemią. Przy dużym nasileniu zjawiska ostre górskie szczyty wyglądają jak płaskie pasmo. Dzieje się tak przy silniejszym załamania światła w cienkiej warstwie powietrza, w której występuje nietypowy rozkład temperatury w zależności od wysokości. Kąt, o jaki promień światła ulega zakrzywieniu, zależy od odległości, jaką pokonuje ono w powietrzu. Im dłużej przebiega w warstwie powietrza o silnej refrakcji, tym silniej się załamuje. Światło biegnące od niższego punktu pokonuje dłuższy dystans w obrębie tej warstwy w porównaniu z punktem położonym wyżej, a zatem ulega silniejszemu zakrzywieniu. Obserwujemy wówczas zniekształcenie obrazu gór w taki sposób, że niższe szczyty i zbocza gór są podniesione silniej niż wyższe wierzchołki. Powstawanie tego zjawiska przedstawiają poniższe rysunki.
Przykładem jest widok Tatr z Łychowa Gościeradowskiego z 3.11.2022. Po rozciągnięciu zdjęcia w pionie wyraźniej zarysowują się wierzchołki, pasujące do ich spodziewanego układu.
Refrakcja a zasięg widoczności
gdzie h – wysokość obserwatora, R – promień Ziemi.
Poniższa tabela przedstawia zasięg widoczności z punktów położonych 100 i 1000 metrów nad ziemią dla terenu równinnego.
| wysokość nad ziemią [m] | współczynnik refrakcji | zasięg widoczności [km] | procentowy wzrost zasięgu |
| 100 | 0 | 35,70 | 0,00% |
| 100 | 0,13 | 38,27 | 7,21% |
| 100 | 0,3 | 42,66 | 19,52% |
| 1000 | 0 | 112,88 | 0,00% |
| 1000 | 0,13 | 121,02 | 7,21% |
| 1000 | 0,3 | 134,92 | 19,52% |
Refrakcja w symulacjach widoczności
Wpływ refrakcji atmosferycznej można dość dobrze odwzorować w niektórych programach do wizualizacji panoram widokowych, jeśli nie ulega ona znacznym zmianom na linii widzenia pomiędzy obserwatorem a widzianym obiektem. Problem pojawia się w warunkach zapewniających znaczne zwiększenie refrakcji, na które czeka wielu dalekich obserwatorów. Mowa tu o inwersji temperatury, a ta występuje w warstwie powietrza o niewielkiej grubości. Jeśli pomiędzy obiektem a obserwatorem światło pokonuje relatywnie dużą różnicę wysokości, część dystansu przebędzie poza warstwą inwersyjną. Występuje wtedy znaczne zróżnicowanie refrakcji, dochodzi do pionowych zniekształceń obrazu, który wygląda inaczej niż przy jednorodnej refrakcji. Obliczony na podstawie fotografii wykonanej w takich warunkach średni współczynnik refrakcji przyjmuje wówczas różne wartości dla obiektów o różnej wysokości. Nie da się tego przedstawić programem, który umożliwia ustawienie tylko jednej, stałej wartości współczynnika refrakcji.
W programach tworzących symulacje panoram widokowych możliwe jest uwzględnienie refrakcji atmosferycznej w następujące sposoby:
- dokładne obliczenie przebiegu promieni światła na podstawie podanego pionowego profilu temperatury i wilgotności powietrza
- zwiększenie promienia Ziemi
- wykonanie symulacji z większej wysokości nad poziomem terenu
- zwiększenie wysokości obserwowanego punktu
Taką możliwość ma program atm-raytracer, który tworzy wizualizację widoku na podstawie podanych parametrów atmosfery. Uwzględnia zmiany temperatury i wilgotności powietrza z wysokością, a więc również zmienność refrakcji. Istnieją jednak istotne ograniczenia związanych z jego zastosowaniem: zakłada stały profil pionowy atmosfery (w rzeczywistości może się on zmieniać wzdłuż linii obserwacji) i oczywiście wymaga podania parametrów powietrza na różnych wysokościach, podczas gdy tak naprawdę nie wiemy, jakie one dokładnie były w momencie i miejscu obserwacji. Można tu wykorzystać pomiary radiosondażowe atmosfery, które są wykonywane za pomocą balonów meteorologicznych, jednak są one wykonyane zaledwie 2 razy na dobę w punktach oddalonych od siebie o setki kilometrów. Dają one ogólny pogląd na występujące warunki, ale to za mało, by wiernie odtworzyć widok przy dużej zmienności refrakcji w czasie i przestrzeni.
Metoda ta bardzo dobrze odwzorowuje wpływ stałej refrakcji na całą panoramę, niezależnie od ukształtowania terenu czy odległości, na jaką rozciąga się widok. Wykorzystuje ona następujące założenie – matematycznie efekt refrakcji atmosferycznej jest taki, jakby światło przebiegało po linii prostej, a Ziemia miała promień krzywizny równy r = R / (1 – k), gdzie R – promień Ziemi, k – współczynnik refrakcji. Prawdopodobnie jest stosowana w generatorze panoram U. Deuschle. Domyślnie jest w nim zastosowana wartość k=0,13, można ją jednak zmienić, wpisując jako zasięg symulacji frazę X_RCY, gdzie X – zasięg symulacji w km, Y – współczynnik refrakcji – (np. 300_RC0,3 dla zasięgu symulacji 300 km i wsp. refrakcji 0,3).
Ten sposób działa w każdym programie, który ma możliwość wykonania symulacji z dowolnej wysokości nad ziemią, jednak ma istotną wadę. Widok znad powierzchni Ziemi różni się od tego, jaki powstaje w wyniku refrakcji – inaczej zmieniają się kąty względem płaszczyzny poziomej, pod którymi widać poszczególne elementy panoramy. Refrakcja sprawia, że obiekty widoczne są wyżej i podniesienie to wzrasta z odległością. Natomiast w przypadku zwiększania wysokości obserwatora kąt pomiędzy obiektem a płaszczyzną poziomą wzrasta w coraz mniejszym stopniu wraz ze wzrostem odległości – jest więc odwrotnie niż w przypadku refrakcji. Nie da się zatem zobrazować tą metodą wpływu refrakcji na całą panoramę.
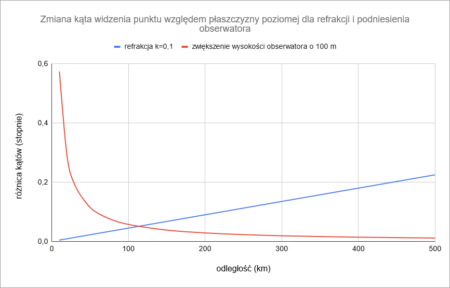
Zastosowanie metody ogranicza się do zobrazowania pozornego zwiększenia wysokości widocznego obiektu względem innego, położonego bliżej – zazwyczaj najlepiej wybrać najdalszy punkt widoczny przed tym obiektem. W tak określonym układzie punktów sprawdza się ona bardzo dobrze, musimy jednak pominąć części panoramy położone w odległościach istotnie różniących się od odległości do tych punktów.
Wysokość, o jaką należy podnieść miejsce wykonania symulacji, określa przybliżony wzór:
gdzie k – współczynnik refrakcji (lub jego różnica), d1 – odległość do bliższego punktu, względem którego określamy podniesienie, d2 – odległość do dalszego obserwowanego punktu, R – promień Ziemi.
Można go przekształcić, wprowadzając stosunek odległości n = d2 / d1:
Wynika z niego, że wysokość jest odwrotnie proporcjonalna do stosunku odległości do obu punktów.
Wielkość błędu tej metody można określić dla każdego punktu widocznego na symulacji za pomocą kąta, o jaki punkt jest na niej przesunięty w porównaniu z symulacją wiernie odzwierciedlającą wpływ refrakcji. Innymi słowy jest to różnica kąta, pod jakim na obu symulacjach widoczny jest punkt względem płaszczyzny poziomej dla miejsca wykonania symulacji. Przesunięcie wynikające z różnicy tych metod występuje zawsze w kierunku pionowym, azymut nie ulega zmianie. Miarę tego kąta wyrażoną w radianach określa wzór:
gdzie Δα – kąt przesunięcia (podniesienia) punktu względem prawidłowego odwzorowania refrakcji, D – odległość do punktu, względem którego określamy przesunięcie, d – odległość do punktu, dla którego wykonujemy obliczenia, h – wysokość punktu, z którego jest wykonana symulacja, k – współczynnik refrakcji, R – promień Ziemi.
Przeliczając kąt na stopnie, a następnie mnożąc przez rozdzielczość symulacji w pikselach na stopień, otrzymamy wielkość tego przesunięcia w pikselach.
Wzór jest odpowiedni dla małych kątów – dla bardzo małych odległości, porównywalnych z wysokością podniesienia miejsca wykonania symulacji kąt jest duży i należy zastosować bardziej skomplikowaną wersję wzoru bez przybliżeń funkcji trygonometrycznych.
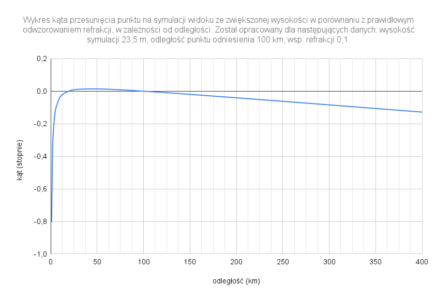
Wykres przedstawia zależność błędu metody od odległości, a dokładnie kąt przesunięcia punktu widzianego z wysokości 23,5 m w porównaniu z widokiem przy refrakcji o współczynniku 0,1, przesunięcie to jest określone względem punktu oddalonego o 100 km. Wysokość ta została obliczona tak, aby odpowiadała refrakcyjnemu podniesieniu punktu oddalonemu o 100 km w porównaniu z punktem w odległości 30 km – dlatego w tych miejscach kąt wynosi 0. Wracając do oznaczeń w wyżej wymienionych wzorach – w tym przypadku d₁ = 30 km, d₂ = 100 km. Z wykresu (i wzoru) wynika, że jeśli utworzymy symulację dla wysokości H(obs) obliczonej za pomocą powyższego wzoru, tereny położone bliżej niż d₁ będą zaniżone (i zaniżenie to gwałtownie rośnie dla małych odległości), pomiędzy d₁ a d₂ – zawyżone, natomiast dalsze od d₂ znowu ulegają zaniżeniu w porównaniu z rzeczywistym efektem działania refrakcji.
Przydaje się ono m.in. w Heywhatsthat do wyznaczenia obszarów widoczności obiektu przy zwiększonej refrakcji. Sytuacja jest tu analogiczna do omawianej powyżej, ale symulację tworzymy w drugą stronę. Alternatywnie można obliczyć podniesienie obserwowanego obiektu za pomocą wzoru:
Tę metodę również należy rozpatrywać tylko dla określonego układu punkt obserwacyjny – punkt pośredni – punkt obserwowany, wysokość podniesienia także zależy od stosunku odległości do obu tych punktów:
Wyprowadzenie wzorów znajduje się na stronie Obliczenia.
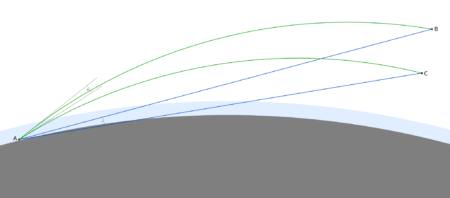
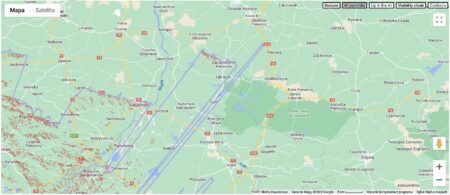
Sprawdźmy, jak w praktyce wyglądają efekty zastosowania poszczególnych metod na przykładzie widoku Tatr z Potoka Wielkiego w woj. lubelskim, wygenerowanego przez symulator U. Deuschle. Dla współczynnika refrakcji 0,22 najdalszy punkt widoczny przed Łomnicą leży w odległości 52 km, natomiast do Łomnicy jest 226,5 km. Podstawiając te dane do wzoru na podniesienie obserwatora, otrzymujemy wysokość 83 m. Jako współczynnik refrakcji musimy podać jego różnicę względem domyślnie stosowanej w tych symulacjach wartości 0,13, czyli 0,09.
Uzyskany za pomocą obu metod widok Tatr wygląda dość podobnie, ale można zauważyć kilka różnic. Wynikają one z wyżej opisanych cech metody z podniesieniem obserwatora – wiernie przedstawiona jest jedynie relacja pomiędzy Łomnicą i szczytami położonymi w podobnej odległości, a terenami oddalonymi o 52 km. Dlatego też: dalsze szczyty wystają nieco mniej, tereny położone dalej niż 52 km, ale bliżej niż Tatry – za wysoko, zaś obszary umiejscowione bliżej są odwzorowane niżej w porównaniu z refrakcją.
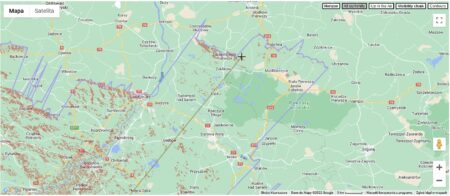
Zobaczmy, jak wygląda symulacja refrakcji przez zwiększenie wysokości obiektu w heywhatsthat.com. Mapy są tam generowane dla standardowego współczynnika refrakcji ok. 0,14, więc do obliczeń przyjęto różnice względem tej wartości. Mapa po stronie lewej jest utworzona dla faktycznej wysokości szczytu 2634 m n.p.m., natomiast mapa po prawej dla 2882 m n.p.m. – taka wysokość, czyli zwiększona o 248 m, powinna odwzorować refrakcję o wsp. 0,22 w porównaniu z 0,14 dla obserwacji z Potoka Wielkiego (odległości do obu punktów wymagane w obliczeniach są takie same, jak powyżej).
Zwiększenie wysokości obrazuje w pewnym zakresie zasięg widoczności przy zwiększonej refrakcji, ale tu także są ograniczenia związane z odległościami. Dla bardziej odległych terenów refrakcja byłaby zaniżona, a dla bliższych zawyżona, istotne znaczenie ma też odległość do najdalszego terenu widocznego przed Tatrami. Metoda ma więc głównie zastosowanie lokalne, do analizy widoczności na niewielkim obszarze.
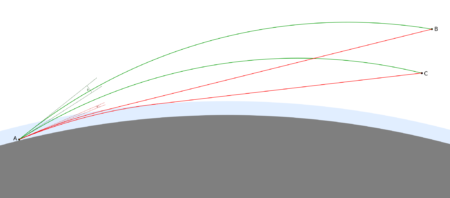
Poniższy profil przedstawia porównanie linii obserwacji Łomnicy z Potoka Wielkiego. Brązowa linia jest dla współczynnika refrakcji 0,22 i wysokości szczytu 2634 m n.p.m., natomiast czerwona dla wsp. 0,14 i wysokości szczytu 2882 m n.p.m. Linie przecinają się w punkcie oddalonym od Potoka o 52 km, ponieważ dla tego punktu została obliczona wysokość podniesienia szczytu.
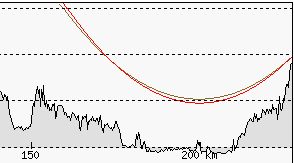
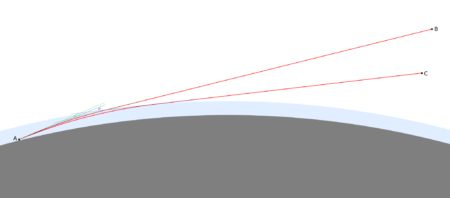
Dla większej odległości takiej samej refrakcji odpowiada większe podniesienie obiektu. Tak to wygląda na przykładzie Łomnicy widzianej z rumuńskiego szczytu Curcubăta Mare, oddalonego o 358 km. Punkt odniesienia został przyjęty w odległości 158 km – jest to najdalsze widoczne wzniesienie zasłaniające Łomnicę przy standardowej refrakcji. Z obliczeń wynika, że symulacja refrakcji o wsp. 0,22 wymaga zwiększenia wysokości Łomnicy o 450 m.
Widać, że zastosowanie takiego samego podniesienia Łomnicy, jak w przypadku Potoka Wielkiego, nie odpowiada refrakcji względem wybranego punktu odniesienia, znajdującego się 158 km od rumuńskiego szczytu i 200 km od Łomnicy – niebieska linia wyraźnie odbiega w tym miejscu od brązowej. Czerwona linia ustawiona na szczyt Łomnicy podniesiony o 450 m przecina linię brązową w wybranym punkcie, tak więc prawidłowo odzwierciedla wpływ refrakcji względem tego punktu.




Świetny materiał. Duża porcja wiedzy.
Interesujące opracowanie, bardzo dobrze opisuje zagadnienie i zależności.
Ostatnio spotkałem się z informacją, że to samo zjawisko dyfrakcji atmosferycznej powoduje przesunięcie w czasie rzeczywistego momentu równonocy, a tym samym początku wiosny lub początku jesieni, ze względu na bezpośredni wpływ na godzinę obserwowalnego wschodu lub zachodu słońca.
Dodatkowo chciałbym zasugerować koncepcję fotografowania odległych horyzontów. Może zastosować metodę astrofotograficzną? Nagranie sekwencji jako klip filmowy, następnie zestakować materiał z wybranych klatek np. w „Autostakkert”
Pozdrawiam
Zgadza się, lecz jest to refrakcja, a nie dyfrakcja. Jeśli chodzi o tę metodę rejestracji obrazu, niezbyt dobrze sprawdza się w takim zastosowaniu. Po połączeniu klatek ostrość ulega pogorszeniu i potem trzeba zastosować bardzo silne wyostrzanie, powodujące artefakty. W dodatku jakość obrazu na filmie jest gorsza, a rozdzielczość mniejsza w porównaniu ze zdjęciem w formacie raw.
Oczywiście, że mówimy o refrakcji, w poprzednim komentarzu to przejęzyczenie.
Nie mogę jednak się zgodzić ze stwierdzeniem, że klip filmowy ma gorszą jakość z założenia. Robiąc nagranie np. kamerą astrofotograficzną używa się formatu bezstratnego np. *.ser w 16bit w pełnej rozdzielczości matrycy. Tak naprawdę można byłoby wykonać również serię zdjęć z bardzo krótkimi czasami naświetlenia w formacie tiff albo też raw (tylko że zajmuje to na dysku dużo więcej miejsca). Zdjęć można wykonać np. 100-200. W astrofotografii planet zwalczając tzw. słaby seeing wykonuje się ich jeszcze więcej. Przy składaniu specjalne programy selekcjonują najlepsze pod względem jakości ujęcia i tylko te wykorzystuje się do „stacka”.
Po złożeniu takiej ilości klatek obraz można poddać bardzo mocnej obróbce wyostrzania bez wyraźnych artefaktów czy wzmocnienia szumów. To zaleta tej metody, sprawdzona w astro 1000 krotnie.
Nie mogę dopatrzeć się przeciwskazań w zastosowaniu dziennym, zwłaszcza, że dotyczy to zasadniczo tych samych zagadnień: atmosferycznych zakłóceń obrazu odległego obiektu.
Oczywiście planuję potwierdzić te założenia w praktyce, jak tylko powstaną odpowiednie warunki pogodowe.
Pozdrawiam serdecznie
Testowałem tę metodę za pomocą lustrzanki z matrycą 24 Mpx. Kamera astrofotograficzna byłaby pozbawiona wad związanych z formatem i kompresją obrazu, lecz rozmiar obrazu nadal będzie mały. Być może materiał z takiej kamery byłby finalnie pozbawiony artefaktów, natomiast wykorzystując lustrzankę nie udało mi się ich uniknąć. Może to wynikać z dużo większego niż w przypadku obserwacji nieba rozmywania się i falowania obrazu w powietrzu. Dystans, jaki światło pokonuje w gęstej warstwie atmosfery, sąsiadującej z gruntem o zróżnicowanej temperaturze, jest znacznie mniejszy, jeśli patrzymy stromo w górę. Kolejny problem pojawia się, jeśli fotografujemy o świcie lub zmierzchu – wtedy jedną klatkę trzeba naświetlać kilka sekund i pozyskanie dużej ich liczby byłoby trudne, a obserwowany obiekt pojawia się czasem dosłownie na chwilę. Długie naświetlanie powoduje też większe rozmycie obrazu – kumulują się przesunięcia obrazu spowodowane wpływem atmosfery.
O wiele lepsze efekty uzyskałem, fotografując w ten sposób Jowisza i Saturna.
Zgadzam się, że 300 km nisko w atmosferze to duży problem. Ale lustrzanka nie rozwiązuje tego problemu. Rejestrujemy różne ujęcia pofalowanego zniekształconego obrazu i żadne z pojedynczych ujęć nie jest zadawalające, a obróbka wyostrzania pojedynczego ujęcia jest bardzo ograniczona ze względu na szum matrycy i artefakty. Dłuższe naświetlanie wymagane o świcie daje uśredniony rozmyty obraz. Dlatego myślę, że zastosowanie teleskopu o trochę większej światłosile (choćby 150×600) w powiązaniu z astrokamerą i podwyższonym gainem, pozwoliłoby na wykonanie wielu klatek z krótszym czasem, rzędu 0,1 sek. Stakowanie z jednej strony sumuje nam zebrane światło, więc czas naświetlania możemy skrócić, a z drugiej strony wybór klatek z tymi najlepszymi momentami pojawiających się konturów oraz z możliwością dużej redukcji szumu tą metodą z możliwością zastosowania mocniejszego wyostrzenia, powinno ogólnie dać szanse na lepszy rezultat. Dzisiejsze astrokamery z rozdzielczością 24 Mpx nie są czymś wyjątkowym, są dostępne dużo lepsze. Zdaje sobię sprawę, że astrokamera „Fullframe” nie jest tania, ale możnaby zastosować z powodzeniem format 4/3″ . Dodatkowo możnaby się pokusić o zastosowanie w ścieżce optycznej korektora ADC, bo dyspersja atmosferyczna też daje tu o sobie znać.
Moją przygodę z astrofotografią również zaczynałem od lustrzanki FF 24Mpx i obróbką najlepszych ujęć pojedyńczej klatki. Obecnie nie wracam do tego. Fotografowanie obiektów astro też czasem musi odbywać się w podobnych trudnych warunkach, bo niektóre obiekty czy planety mamy dostępne na naszej półkuli w pewnych okresach tylko nisko nad horyzontem. Te metody w tych warunkach oczywiście nie pozwalają na uzyskanie dobrego zdjęcia, bo nie mamy dostępnego dobrego obrazu obiektu, ale uzyskanie lepszego rezultatu niż zwykłą metodą myślę że tak.
Pozdrawiam
Trzeba by było spróbować takim teleskopem i kamerą, ja nimi nie dysponuję. Na pewno byłby to cięższy i mniej mobilny sprzęt niż lustrzanka z obiektywem 150-600 mm na fotograficznym statywie.
Jak będę miał okazję to przetestuję tą metodę. Na początek bardziej mobilnym sprzętem: teleskop Maksutova 127×1500 (3,5 kg) + kamera astro + korektor ADC + laptop i lekki statyw. W plecaku się zmieści ;). Zobaczę czy będzie to obiecujące w takim zastosowaniu.
Pozdrawiam
Na szybko wykonane zdjęcie testowe „stack”: kompleks na górze Landeskrone w Görlitz (ok. 8 km, termika powietrza nad dachami całego miasta i wiatr dawały się we znaki)
Zdjęcie wykonane teleskopem 127 mm / f=1500 mm)
Jest nieco więcej szczegółów, ale są też artefakty typu halo.
Tak zgadza się, obróbka nieco przesadzona, tak trochę, żeby pokazać, że nawet tak bardzo forsowne potraktowanie zdjęcia jest możliwe w przypadku staka. Wyostrzanie robiłem tylko metodą podnoszenia lokalnych kontrastów i dość mocno, stąd halo, ale można to zrobić lepiej np. narzędziami programu Registax 6. Ale myślę,że nawet na tej szybkiej próbce (wykonanej na chybotliwej podłodze strychu przy szarpiących powiewach wiatru) widać, że potencjał w tej metodzie istnieje dla takich zastosowań. W serii zdjęć pojedynczych widać było dużo zniekształceń konturów, wykrzywień i zanikań elementów. Natomiast po zestakowaniu ok 10% z 500 bardzo krótko naświetlanych klipów, wszystkie elementy jak maszty, anteny i kontury wieży są zdecydowanie lepiej zarysowane. Zachęcam do eksperymentowania w zdjęciach z dalekimi horyzontami ;).
Pozdrawiam
Witam ponownie.
W załączeniu jeszcze jedna wersja z tego samego klipu video *.ser (raw 16bit), trochę inaczej zestackowanego, staranniej obrobionego narzędziami programu Registax, mniej forsownie, ale z zachowaniem detalu, który się zarejestrował.
Wg mnie efekt jest lepszy, detal i szczegóły w światłach też korzystniej, brak efektu halo.
Wiele zależy od przyjętych parametrów. W Autostakkert np. istotne było zaznaczenie opcji „global” zamiast „local”, przyjęte punkty do alignacji.
Również wymaga wyczucia użycie narzędzi dekonwolucji Registaxa.
Sam kiedyś wykonałem to zdjęcie lustrzanką i obiektywem Tamron 150-600, zanim wszedłem w astro. Teraz z ciekawości powtórzyłem to ujęcie stosując inne podejście. Obecny efekt jest lepszy, tamtą metodą nie uzyskałem akceptowalnego obrazu.
Może będzie to inspiracją dla innych zainteresowanych tym tematem.
Pozdrawiam serdecznie
Metoda ma potencjał, choć wymaga dopracowania – tutaj typowego halo już nie ma, ale zamiast niego są zielonkawe obwódki wokół masztów na tle nieba i mała plamka w podobnym kolorze na niebie po prawej stronie wieży.
Czy taką kamerkę można podłączyć do zwykłego obiektywu fotograficznego i czy ma ona ekran z podglądem obrazu? Jeśli tak, to rozwiązałoby problem noszenia dużej ilości dodatkowego sprzętu – do standardowego zestawu aparat+obiektyw+statyw wystarczyłoby wziąć samą kamerkę i założyć ją, jeśli zdjęcia z aparatu byłyby nieostre. Nie zawsze byłaby taka konieczność – czasami rozmycie obrazu przez powietrze jest minimalne i obraz na 600 mm jest naprawdę ostry. Niestety nie istnieją prognozy, które mogłyby to dokładnie przewidzieć.
Najpierw się wytłumaczę z tych zielonych obwódek. Jest to efekt składania obrazu z dwóch warstw, gdyż niebo obrabiałem osobno z pojedynczej klatki i zestawiałem z obrazem ze stackowania. Na samym zestakowanym zdjęciu nie ma tego. A zabawę z montażem nieba z chmurami podjąłem z tego powodu, że chmury płynęły bardzo szybko i przy 1 minutowym nagraniu rozmywały się.
A teraz odnośnie adaptera: generalnie są odwrotne tzn. z bagnetu do aparatu na wewnętrzny T2. Akurat dla Canona istnieje adapter gniazdo z bagnetem EOS- T2. Gwint T2 to 42×0,75 typowy dla sprzętu astro.
Nie pamiętam takiej hybrydy kamery z podglądem i obsługą nagrywania. Kiedyś coś chyba czytałem, ale to nie jest typowe i tanie. Normalne kamery astro obsługiwane są z jakiegoś laptopa, choćby małego.
Pamiętam moją ścieżkę rozwoju w astro, jest to świetna szkoła pokonywania własnych ograniczeń, obaw wewnętrznych, blokad i granic.
Pamiętam, że też miałem blokadę przed porzuceniem wygodnego wyświetlacza lustrzanki i przesiadką na kamerę z laptopem ;). Ale to była decyzja o pełnych możliwościach w astrofotografii.
Dedykowane kamery ASI są dobre ,ale te z odpowiednią rozdzielczością i większym pikselem drogie. Do adaptera trzeba sobie przeliczyć odpowiedni backfocus i ewentualnie korygować pierścieniami dystansowymi.
Ja używam kamery SVBONY SV405CC – już prawie niedostępna (znalazłem jeszcze 1 ofertę).
Linki:
Do adaptera:
https://teleskopy.pl/@6489?gad_source=1&gclid=CjwKCAjw3624BhBAEiwAkxgTOgIR2Qjszc6viVloFPaKArN3S4YRhbq1jGrFdkyyUs98sBMD7g593RoCDWsQAvD_BwE
Do kamery:
https://www.kaufland.pl/product/470197817/?kwd&source=pla&sid=36016207&utm_source=google&utm_medium=cpc&utm_id=21393699249&gad_source=1&gclid=CjwKCAjw3624BhBAEiwAkxgTOln0uK3tNUyIRhOAQKPOnM2mzMPqep9K4BhrQBR9lbR349UtbZ7gEBoCCngQAvD_BwE
Potrzebne oprogramowanie (darmowe):
SharpCap – obsługa kamery
Autostakkert – stakowanie
Registax 6 – obróbka staka
i coś do końcowej obróbki fotografii.
Pozdrawiam
Dziękuję za odpowiedzi, zapewne będą pomocne dla osób, które rozważają wykorzystanie takiego sprzętu.
Dla porównania zdjęcie – pojedyncza klatka obrobiona analogicznie jak „stackowana”. kompleks na górze Landeskrone Görlitz. (Teleskop 127 mm / f=1500 mm)
Uzupełnienie:
W procesie stackowania w module alignacji możemy ręcznie zaznaczyć punkty konturów masywów górskich, na których nam najbardziej zależy. Będzie to uwzględnione przy nakładaniu wielu ujęć i zmniejszy rozmywanie tych konturów.
I jeszcze odnośnie rozdzielczości obrazu:
z jednej strony teoretycznym ograniczeniem będzie Kryterium Rayleigha, więc efektywna średnica zastosowanej optyki (i jej jakość),
z drugiej strony rozdzielczość matrycy aparatu/kamery.
Jednak zdecydowanie najistotniejszym ograniczeniem rozdzielczości uzyskanego obrazu będzie stan atmosfery, który niweczy dwa pierwsze elementy składowe.
Pozdrowienia