Na zdjęciach widać: nocną panoramę Warszawy i światła masztu RTCN Warszawa/Raszyn
Miejsce obserwacji: schody i taras na gołoborzu na Łysej Górze (Świętym Krzyżu) w Górach Świętokrzyskich:
50,860972°N, 21,047500°E, ok. 583 m n.p.m. – Warszawa
50,860768°N, 21,047419°E, ok. 589 m n.p.m. – komin Ciepłowni Kawęczyn
50,861132°N, 21,047491°E, ok. 578 m n.p.m. (taras) – RTCN Warszawa/Raszyn, panoramy
Odległość: komin Ciepłowni Kawęczyn 156,6 km, wieżowce w centrum Warszawy 152-152,9 km, maszt RTCN Warszawa/Raszyn 135,2 km
Data: 28.05.2023, godz. 0:00 – 2:10
Autorzy: Łukasz Wawrzyszko, Paweł Kłak
Aparat: Canon 6D + Tamron 150-600 mm G2 (Ł. Wawrzyszko), Canon 6D + Sigma 150-500 mm (P. Kłak)
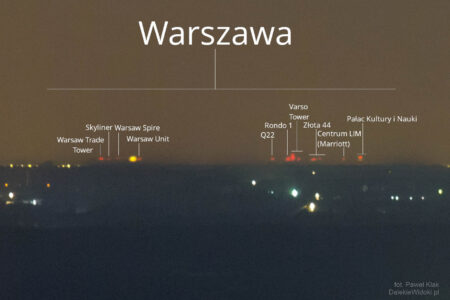
Łysa Góra (Święty Krzyż) w Górach Świętokrzyskich to najdalsze miejsce, z którego została zaobserwowana Warszawa. Najbardziej odległym obiektem, który można dostrzec jest komin Ciepłowni Kawęczyn oddalony o 156,6 km. Po jego lewej stronie widoczne są wieżowce w centrum stolicy położone w odległości 152-153 km, wśród których swą wysokością wyróżnia się Varso Tower – najwyższy wieżowiec w Unii Europejskiej (310 m).
Aktualne zestawienie najdalszych punktów z udokumentowanym widokiem na Warszawę znajduje się na stronie Dalekie obserwacje Warszawy.Po raz pierwszy Warszawę ze świętokrzyskiego gołoborza sfotografował Paweł Kłak o świcie 22.05.2023 r. – widoczne było światło iglicy Varso Tower, będącej najwyższym punktem miasta. Są opublikowane na stronie dalekiewidoki.pl.
Niecały tydzień później – 28.05.2023 r. podjęliśmy (Łukasz Wawrzyszko i Paweł Kłak) próbę ponownej obserwacji, o nieco wcześniejszej porze. Po północy wycelowaliśmy obiektywy w stronę stolicy i na ekranach aparatów ukazały się światła Varso, a także kolejne, podobne czerwone światło obok po prawej stronie – jak się potem okazało – Pałac Kultury i Nauki. Nad zachodnią częścią Starachowic widniało zaś światło komina Ciepłowni Kawęczyn, a to oznaczało nowy rekord odległości obserwacji Warszawy – 156,6 km. Około pół godziny później zza horyzontu niespodziewanie wyłoniły się kolejne światła – w kulminacyjnym momencie było widać aż 10 najwyższych warszawskich wieżowców. Po godzinie 1 ponownie były widoczne tylko pojedyncze obiekty.



Zbliżenie na światła warszawskich wieżowców




Zdjęcia Pawła Kłaka – więcej na stronie dalekiewidoki.pl:
Tak zmieniał się widok w ciągu dwóch godzin:
Animacja na podstawie zdjęć Pawła Kłaka:

Poszczególne obiekty zostały zidentyfikowane z wykorzystaniem pomiarów i obliczeń azymutów. Poniższe zdjęcie z nałożoną mapą zawierającą linie biegnące od Świętego Krzyża do wieżowców pokazuje, że rozmieszczenie świateł pasuje do lokalizacji budynków.
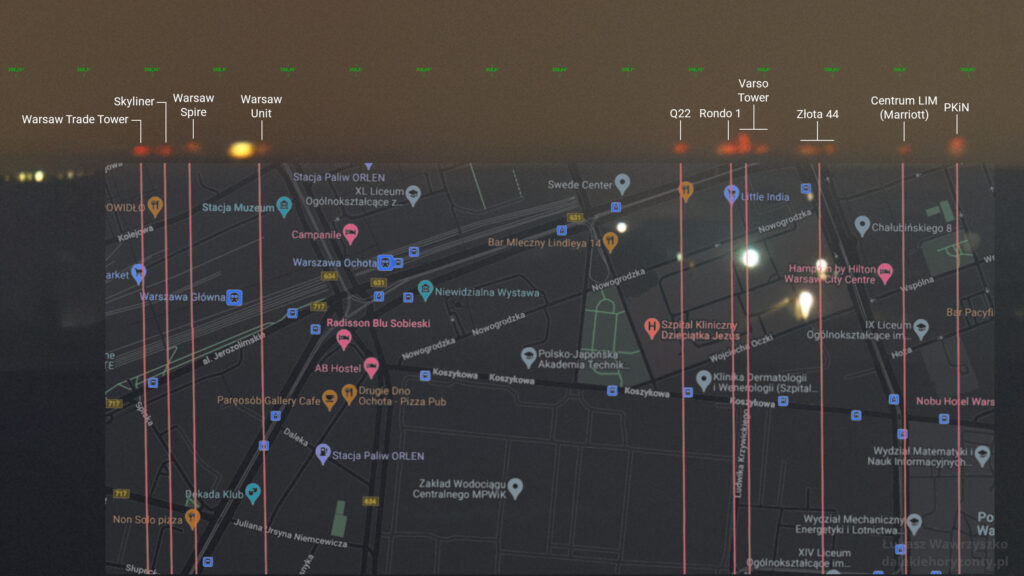
Tabela z lokalizacją i odległościami do poszczególnych obiektów:
| Obiekt | Mapa | Wysokość (m n.p.m.) | Azymut (°) | Odległość (km) |
| Widok z punktu 50,860972°N, 21,047500°E | ||||
| Warsaw Trade Tower | https://goo.gl/maps/XybUH5vUKPYWNpQE8 | 319 | 358,342 | 152,9 |
| Skyliner | https://goo.gl/maps/AhaBtLGHfPhFWfx9A | 307 | 358,359 | 152,3 |
| Warsaw Spire | https://goo.gl/maps/Tj1ELZChwgVuBGm29 | 331 | 358,377 | 152,5 |
| Warsaw Unit | https://goo.gl/maps/DND4F6zQa2B4d4PD7 | 316 | 358,429 | 152,3 |
| Q22 | https://goo.gl/maps/5tF4xpnSAhcZ7oLfA | 309 | 358,738 | 152,9 |
| Rondo 1 | https://goo.gl/maps/3CLtGnEQv5ADWbW66 | 306 | 358,775 | 152,6 |
| Varso Tower | https://goo.gl/maps/pPcJMCstWBwEekMC7 | 424 | 358,787 | 152,1 |
| Złota 44 | https://goo.gl/maps/4iWXAWfTY2izz5q67 | 306 | 358,841 | 152,4 |
| Centrum LIM | https://goo.gl/maps/fZWhzx9LNFKasS9u6 | 295 | 358,902 | 152 |
| Pałac Kultury i Nauki | https://goo.gl/maps/xQCPjmHgCvMDv7LG7 | 352 | 358,942 | 152,5 |
| Widok z punktu 50,860768°N, 21,047419°E | ||||
| komin Ciepłowni Kawęczyn | https://goo.gl/maps/s8LuZck61sZdt4JK8 | 392 | 2,028 | 156,6 |
Z tarasu na gołoborzu na lewo od Warszawy był widoczny jeszcze jeden odległy obiekt – maszt Radiowo-telewizyjnego Centrum Nadawczego Warszawa/Raszyn, oddalony o 135,2 km.



Jak to możliwe, że jednego dnia widać tylko jeden obiekt, a innego znacznie więcej?
Zgodnie z obliczeniami, w standardowych warunkach Warszawa powinna być całkowicie schowana za horyzontem. W pogodne noce występuje jednak zjawisko, które zmienia przebieg światła w atmosferze, umożliwiając zajrzenie nieco dalej niż zwykle „za horyzont”. Mowa o radiacyjnej inwersji temperatury – grunt wypromieniowuje ciepło, ochładza się, a razem z nim przygruntowa warstwa powietrza. Staje się ona chłodniejsza niż powietrze położone powyżej – w takich warunkach występuje silniejsze załamanie światła, dzięki czemu promienie światła mogą dotrzeć nieco dalej, omijając w pewnym stopniu krzywiznę Ziemi.
Zjawisko to może mieć różne nasilenie i zależy przede wszystkim od tego, jak zmienia się temperatura powietrza z wysokością. Więcej na jego temat można przeczytać na stronie Refrakcja atmosferyczna, gdzie między innymi wyjaśniony jest współczynnik refrakcji – parametr określający intensywność załamania światła w atmosferze. Standardowo wynosi on ok. 0,13 – 0,15, natomiast światło na szczycie iglicy Varso powinno być widoczne nad horyzontem dla współczynnika co najmniej 0,3. Z kolei światło na najniższym widocznym na zdjęciach budynku – Centrum LIM – wymaga współczynnika 0,44, czyli światło musi załamać się aż 3-krotnie silniej niż standardowo. Ze względu na niejednorodność atmosfery mowa o uśrednionych współczynnikach dla całego dystansu obserwacji. Z pomiarów temperatury powietrza wykonanych w Legionowie przy pomocy balonu meteorologicznego wynika, że refrakcja znacznie zmieniała się z wysokością, istotnie odbiegając od średnich wartości – dlatego średni, stały współczynnik refrakcji nie odzwierciedla wystarczająco dokładnie rzeczywistych warunków. Do wysokości nieco ponad 100 m nad ziemią występowała silna inwersja temperatury, która powyżej nagle kończyła się i dalej następował stopniowy spadek temperatury zbliżony do tego, jaki ma miejsce w warunkach standardowych. Poniższe wykresy zostały opracowane przez dr. hab. Krzysztofa Strasburgera za pomocą jego własnego programu – dokładny opis na jego stronie.
Aby w standardowych warunkach (wsp. refrakcji 0,14) był widoczny szczyt masztu Centrum LIM, musiałby być wyższy o ok. 190 metrów albo należałoby się wznieść ponad 360 m ponad gołoborze. Natomiast wierzchołek iglicy Varso Tower byłby widoczny po jej podniesieniu o ok. 170 m lub gdyby punkt widokowy na Łysej Górze był wyżej o ponad 125 m.
Więcej o tym, dlaczego widać Warszawę z Gór Świętokrzyskich i skąd wiadomo, że to skupisko świateł to właśnie Warszawa, można przeczytać tutaj: Warszawa z Gór Świętokrzyskich – jak to możliwe?.
Na koniec kilka szerszych ujęć z miejsca obserwacji











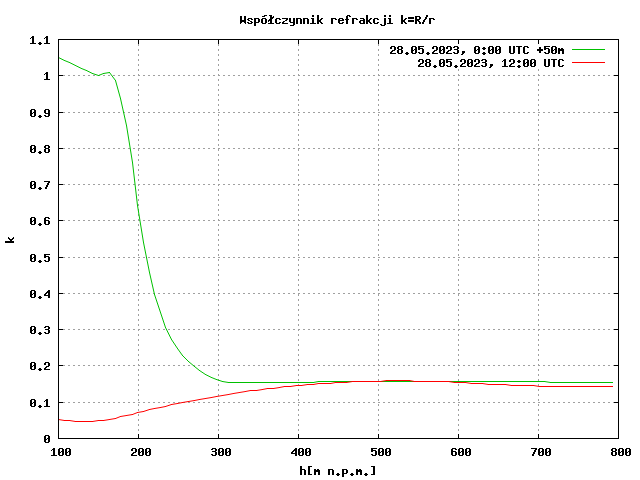
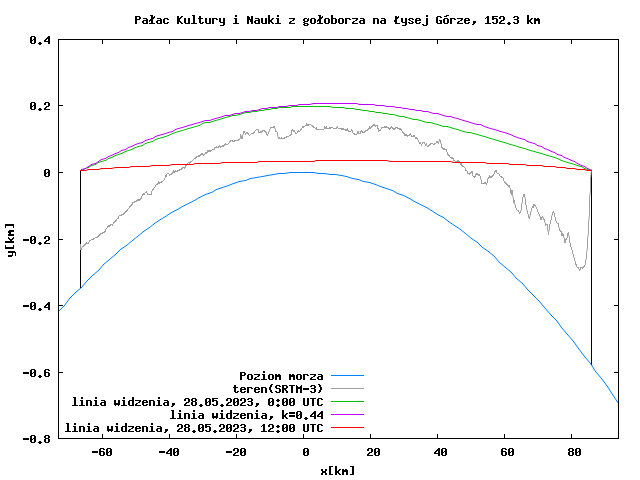


Tamtej nocy wystąpiła superrefrakcja – współczynnik refrakcji osiągał 1, poniżej 150 m n.p.m. Powyżej 250 m n.p.m. wynosił już, w dużym zakresie wysokości, około 0.16, czyli całkiem normalnie. Przeliczyłem to sobie z danymi pomiarowymi z Legionowa. Gdyby światło nie rozpraszało się w atmosferze, a obszar występowania tak silnej inwersji przygruntowej był wystarczająco rozległy, to można by było sięgnąć wzrokiem dowolnie daleko :-).
Podobne warunki były 7 września 2021 r., kiedy to panorama Warszawy została uchwycona z wiaduktu w Kalenicach. Średni współczynnik refrakcji dla całej linii obserwacji wieżowca Warsaw Hub wyniósł ok. 0,5, a pomiar z Legionowa wykazał właśnie ok. 1,2 do wysokości ok. 30 m nad ziemią.
28 maja najsilniejsza refrakcja wystąpiła około godz. 1, a następnie szybko się zmniejszyła i przynajmniej do godziny 2:10 pozostała na mniej więcej stałym poziomie. Podobne zjawisko zaobserwował w kolejną noc Kamil Gołąb – dwie obserwacje to za mało, by mówić o powtarzalności zjawiska, ale warto będzie to sprawdzić.
Można zapytać, w jaki sposób jest obliczany lokalny (zależący od wysokości) współczynnik refrakcji? Chętnie porównałbym go z metodą, którą sam stosuję.
Stosuję do tego arkusz kalkulacyjny wykorzystujący wzór, który znalazłem w anglojęzycznej Wikipedii i innych źródłach: https://dalekiehoryzonty.pl/obliczenia/#5
Wartość pionowego gradientu temperatury można odczytać z radiosondażowych danych pomiarowych. Są też prognozy przedstawiające zależność temperatury od wysokości w formie wykresu, z którego można odczytać przewidywany gradient. Nie są one jednak dokładne, ponieważ prognozowana inwersja radiacyjna zazwyczaj rozciąga się dużo wyżej niż ma to miejsce w rzeczywistości.
Proszę sprawdzić, czy we wzorze na k, we współczynniku 0.00343 nie został przesunięty przecinek. Skonfrontowałem to równanie ze źródłowym, na stronie Waltera Bislina i jeśli przy pionowym gradiencie temperatury pojawia się współczynnik 0.01, to wyraz stały powinien być jeszcze 10 razy mniejszy.
A tak poza tym… to ten wyraz stały wcale nie jest stały, choć być może stanowi tzw. rozsądne przybliżenie.
Z rozważań wychodzących z równania Clausiusa-Mossottiego, po kilku uproszczeniach, usprawiedliwionych dla współczynnika załamania światła tylko trochę większego od 1 i przekształceniu wzoru na odwrotność krzywizny linii widzenia (r), otrzymuję
1/r=[a/(2ek)](p/T^2)[(-T/p)(dp/dh)+dT/dh],
gdzie a to polaryzowalność elektronowa (traktuję ją jako parametr empiryczny). e – przenikalność elektryczna próżni, k -stała Boltzmanna, p -ciśnienie i T – temperatura. Z kolei dp/dh i dT/dh oznaczają pionowe gradienty ciśnienia i temperatury. „Wyraz stały” musi być zatem równy (-T/p)(dp/dh), być może pomnożony przez jakiś współczynnik, wynikający z takiego a nie innego doboru jednostek.
We wzorze jest 0,0343, tak jak na stronie Waltera, gdzie współczynnik ten został wyrażony jako g/RS, czyli iloraz przyspieszenia ziemskiego i stałej gazowej dla powietrza. Po dodaniu jeszcze jednego zera po przecinku (0,00343) wychodzą bardzo małe wartości współczynnika refrakcji, nawet ujemne przy gradiencie temperatury -0,65 K/100 m.
Oczywiście chodzi o odwrotność promienia krzywizny linii widzenia, a nie o odwrotność krzywizny :-).
A skoro juz piszę… Gdzie można znaleźć coś o czytaniu tych wykresów z sondowań radarowych? Dla mnie stanowią zagadkę – ich osie nie są opisane i wydaje mi się, że jest na nich wiele różnych informacji. Dla nie-meteorologa to jest wiedza tajemna :-). Przynajmniej dane z balonów meteorologicznych mają formę przejrzystych tabel i z nimi problemów nie mam. Może dałoby się znaleźć też radarowe w podobnej postaci?
Nie korzystałem z takich wykresów. Używam tylko wykresów i tabel zawierających dane z balonów oraz prognoz w formie podobnych wykresów, z opisanymi osiami.
Proszę uważać z jednostkami! Rozumiem już, skąd wziął się współczynnik 0.01 przed gradientem temperatury – gradient ten jest wstawiany w jednostach K/100m (lub °C/100m – to jeden pies), natomiast stała 0.0343K/m powinna mieć nadal taką właśnie wartość. W opisie obliczeń (tu, na dalekich horyzontach) jest błędne 0.00343 – zapewne jako zwykła literówka (cyfrówka?). Dodam jeszcze, że gdy wstawiłem do mojego wzoru temperaturę 273 K, ciśnienie 1013 hPa i jakiś typowy jego gradient na poziomie morza, to wyszło mi 0.0341K/m, czyli we wzorze Waltera Bislina faktycznie mamy rozsądne przybliżenie.
Współczynnik 503, stojący z przodu całego wzoru na współczynnik refrakcji, ma jednostkę m*K/mbar, a to znaczy, że ciśnienie trzeba wstawiać w milibarach, a nie w hektopaskalach, choć tutaj względny błąd jest marginalny – około 1%. Też to sprawdziłem – przy 1000 mbar, temperaturze 0°C i „typowym” gradiencie temperatury -0.65°C/100m, współczynnik refrakcji wychodzi rówy 0.19 – czyli znowu całkiem przyzwoicie. Nie wiem, co jest w arkuszach kalkulacyjnych, ale do opisu wkradło się kilka nieścisłości, które chyba warto poprawić.
No, ale rozgadałem się o refrakcji, a nawet nie pogratulowałem, chociaż powinienem. To jet rewelacyjna obserwacja – poprawiliście, z Pawłem Kłakiem, dotychczasowy rekord odległości, z której widziano Warszawę, o ponad 50 km!
Rzeczywiście na stronie o krzywiźnie Ziemi i w opisie obliczeń było to niepotrzebne zero. Dziękuję za wychwycenie tej „cyfrówki”. W pozostałych miejscach (w tym m.in. na stronie o refrakcji) i w arkuszu kalkulacyjnym jest dobrze. O jednostkach pamiętam i zgadzają się, ale dla uproszczenia pominąłem je w tym opisie, który jest tylko wyjaśnieniem formuł zawartych w arkuszu. Milibar to to samo, co hektopaskal (1 bar = 105 Pa = 1000 hPa), więc można je stosować zamiennie.
Słusznie, pomyliłem 1 bar z 1 atmosferą (1013 hPa). Oj, skleroza na starość dokucza :-).
dlaczego na zdjęciach nie ma zgodnego z krzywizną ziemi odchylenia obiektów?
Tutaj na obraz wpłynęło niejednorodne załamanie światła, które powoduje dużo większe zniekształcenia (spłaszczenie) obrazu. Przy bardziej jednorodnym pionowym profilu temperatury można byłoby stwierdzić to odchylenie, obserwując obiekty położone w różnych odległościach. Dobrym przykładem są Tatry widziane np. z Wyżyny Lubelskiej – np. z Potoka Wielkiego. Gerlach (2655 m n.p.m.), mimo że jest wyższy, widoczny jest niżej niż Lodowy Szczyt (2628 m n.p.m.). Dzieje się tak właśnie ze względu na odchylenie powierzchni Ziemi spowodowane jej krzywizną – jest odchylona „do tyłu”, więc obiekty położone w większej odległości widoczne są niżej w stosunku do płaszczyzny poziomej dla obserwatora w porównaniu z bliższymi obiektami.