Pomiary refrakcji atmosferycznej na zdjęciu

Wyznaczanie współczynnika refrakcji na podstawie zdjęcia

Na podstawie zdjęcia można oszacować średni współczynnik refrakcji atmosferycznej, mierząc wysokość najniższego widocznego punktu obiektu.

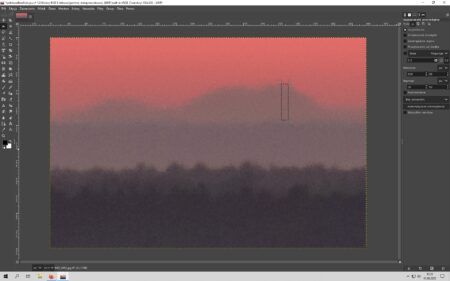
W tym celu musimy zmierzyć na zdjęciu wysokość widocznego fragmentu obiektu. Można to zrobić np. w programie Gimp za pomocą zaznaczenia prostokątnego. Poniższa ilustracja przedstawia taki pomiar na przykładzie Lodowego Szczytu widzianego z Potoka Wielkiego na Wyżynie Lubelskiej. Punktem o znanej wysokości jest wierzchołek góry, więc rysujemy zaznaczenie od wierzchołka, w dół, do najniższego punktu góry widocznego poniżej wierzchołka.

W opcjach narzędzia po prawej stronie podany jest rozmiar zaznaczenia. W tym przypadku długość dłuższego boku zaznaczenia oznacza wysokość widocznej części Lodowego Szczytu – 52 piksele.

Następnie przeliczamy piksele na metry za pomocą następującego wzoru:

$h=\dfrac{p}{l} \cdot \alpha \cdot d$

gdzie h – wysokość widocznej części obiektu w metrach, p – wysokość widocznej części obiektu w pikselach, l – długość boku zdjęcia (pełnego kadru) w pikselach, α – kąt widzenia obiektywu w radianach, d – odległość do widocznego obiektu w metrach. Podajemy kąt widzenia dla tego boku matrycy, dla którego podaliśmy wartość l.
Obliczenia można wykonać np. za pomocą arkusza kalkulacyjnego, w którym wystarczy wpisać ogniskową obiektywu w przeliczeniu na matrycę pełnoklatkową, a także wartości p, l oraz d.
Powyższe zdjęcie zostało zrobione aparatem Canon 6D z obiektywem o ogniskowej 600 mm. Szerokość pełnego kadru wynosi 5472 piksele, kąt widzenia na dłuższym boku matrycy wynosi 3,4367°, czyli 0,05998 rad. Odległość do Lodowego Szczytu to 227,6 km. Podstawiamy te wartości do wzoru:

h = (52 px / 5472 px) * 0,05998 (rad) * 227600 m ≈ 130 m

Oznacza to, że widoczna część Lodowego Szczytu ma wysokość 130 m.
Teraz wartość h należy odjąć od wysokości n.p.m. najwyższego punktu obiektu. Lodowy Szczyt ma 2628 m n.p.m., więc odejmujemy od niego 130 m: 2628 – 130 = 2498. Tak więc najniższy widoczny punkt tej góry znajduje się na wysokości 2498 m n.p.m.

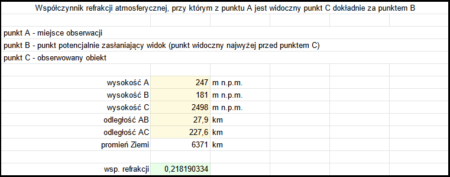
Następnie przeliczamy to na współczynnik refrakcji. Wymaga to wyznaczenia odległości do najdalszego punktu (punktu B) widocznego przed Lodowym Szczytem i jego wysokości. Jest to dość skomplikowane – postępujemy identycznie jak w przypadku wyznaczania minimalnego współczynnika refrakcji zgodnie z opisem, ale jako wysokość punktu C wpisujemy obliczoną wartość 2498 m n.p.m.
W tym przypadku punkt B znajduje się w odległości 27,9 km, na wysokości 181 m n.p.m. (jest to wysokość wierzchołków drzew widocznych poniżej Tatr).
Za pomocą arkusza kalkulacyjnego otrzymujemy wartość współczynnika refrakcji ok. 0,218.

Pomiar wysokości pozornego podniesienia obiektu

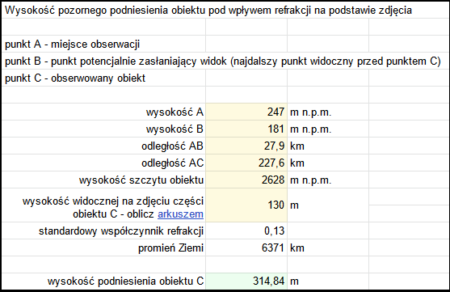
Można też obliczyć wysokość, o jaką został pozornie podniesiony obserwowany obiekt pod wpływem refrakcji. W tym celu – jak wyżej – mierzymy wysokość widocznej części szczytu – w naszym przykładzie jest to 130 m. Następnie liczymy podniesienie obiektu za pomocą arkusza kalkulacyjnego – część „Wysokość pozornego podniesienia obiektu pod wpływem refrakcji na podstawie zdjęcia”.
Analogicznie do powyższych obliczeń współczynnika refrakcji, wymaga to podania odległości do najdalszego punktu (punktu B) widocznego przed Lodowym Szczytem i jego wysokości, które wyznaczamy tą metodą. Po wprowadzeniu danych do arkusza otrzymujemy wartość ok. 315 m. Oznacza to, że Lodowy Szczyt musiałby być o 315 m wyższy, żeby był tak samo widoczny przy standardowej refrakcji atmosferycznej.