1 stycznia 2023 r. Tatry zostały po raz pierwszy zaobserwowane z polskich nizin, a dokładnie z Góry Kamieńskiej będącej hałdą bełchatowskiej kopalni węgla, znajdującej się na Nizinie Mazowieckiej. Czterech pasjonatów dalekich obserwacji z różnych zakątków kraju – Mateusz Cieślicki, Grzegorz Jagusiak, Paweł Kłak i Krzysztof Ninard, uwieczniło na fotografiach najwyższe szczyty Tatr Wysokich, w tym oddalonego o 232 km Gerlacha. Zdjęcia można zobaczyć na stronie https://dalekiewidoki.pl/2023/01/tatry-z-g-kamienskiej.html.
Jest to jedna z najdalszych obserwacji Tatr z Polski – pełna lista polskich rekordów dalekich obserwacji znajduje się na stronie Najdalsze obserwacje z Polski.
Gdyby Ziemia nie miała atmosfery, światło rozchodziłoby się po linii prostej i taka obserwacja byłaby nierealna, co więcej – widok nie jest możliwy także w standardowych warunkach w atmosferze, gdyż na przeszkodzie stoi krzywizna Ziemi oraz wzniesienia położone pomiędzy Górą Kamieńską a Tatrami. Udało się to dzięki większej niż zwykle refrakcji atmosferycznej, czyli ugięciu (załamaniu) światła w powietrzu. Prognozy przewidywały inwersję temperatury od gruntu do wysokości kilkuset metrów n.p.m., a w takich warunkach gęstość powietrza szybciej niż zwykle maleje ze wzrostem wysokości, co sprawia, że światło załamuje się silniej.
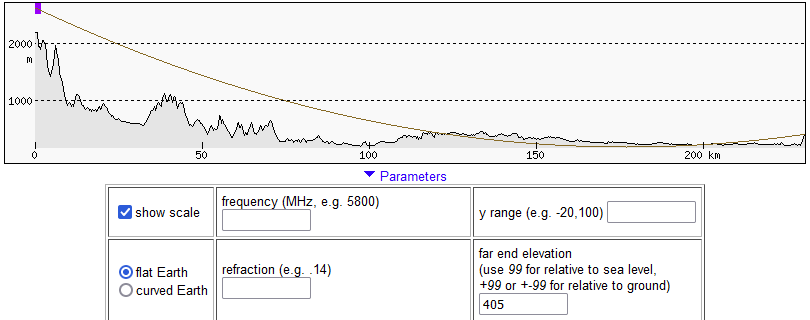
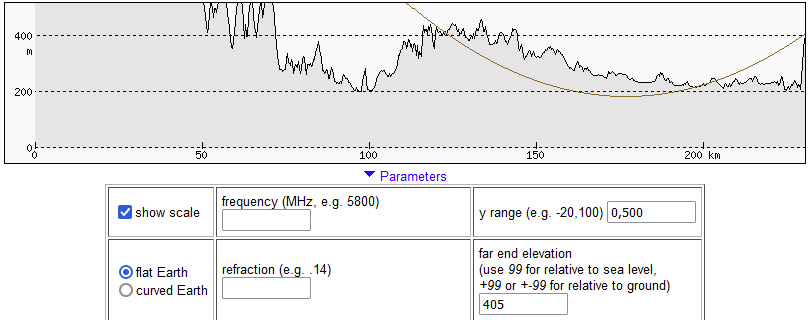
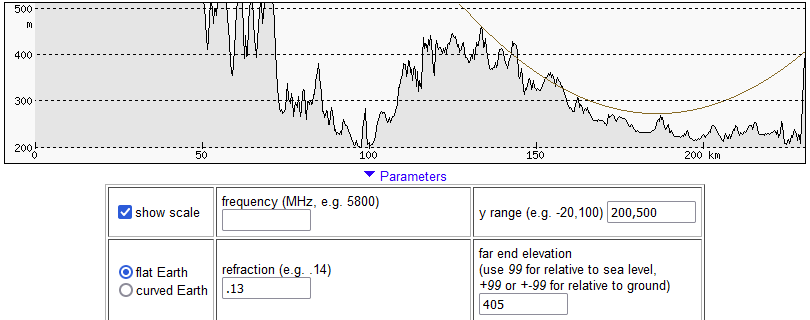
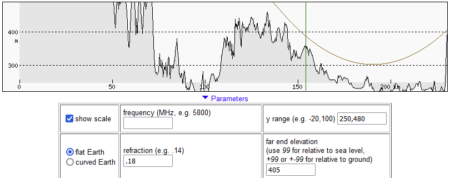
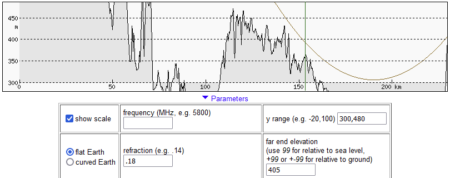
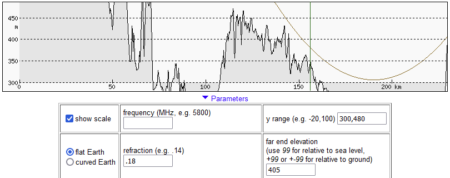
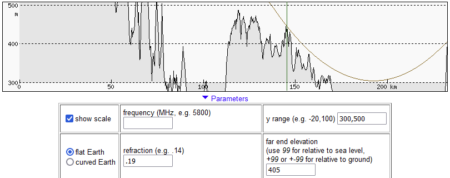
Poniższe ilustracje przedstawiają przebieg linii widzenia Łomnicy z Góry Kamieńskiej i zostały wykonane za pomocą heywhatsthat.com. Pokazują one, jak ukształtowanie terenu na linii obserwacji zasłaniałoby widok, gdyby światło rozchodziło się po linii prostej, a także przy refrakcji atmosferycznej o standardowej wielkości.
Wyznaczanie minimalnego współczynnika refrakcji wymaganego do obserwacji
Czy można dokładnie policzyć, jak bardzo musi się zwiększyć refrakcja, żeby widoczność była możliwa? Tak, ale musimy pamiętać o pewnych ograniczeniach, jakimi obarczone są te analizy. Przede wszystkim powietrze jest niejednorodne i refrakcja zmienia się w przestrzeni. Jej wielkość określamy za pomocą współczynnika refrakcji, zdefiniowanego jako iloraz promienia krzywizny Ziemi i krzywizny łuku, po którym biegną promienie światła. Nie znamy jego dokładnych wartości w każdym punkcie na linii obserwacji, musimy więc przyjąć uproszczenie zakładające jego stałą wartość – jest to jego średnia (efektywna) wartość z całej linii obserwacji. Można go obliczyć za pomocą arkusza kalkulacyjnego, w którym podajemy wysokość n.p.m. miejsca obserwacji, obserwowanego szczytu oraz najdalszego punktu widocznego przed tym szczytem, a także odległość z miejsca obserwacji do obu tych punktów. Arkusz ten wykorzystuje fakt, iż przy minimalnej refrakcji zapewniającej widoczność, wszystkie trzy wymienione punkty leżą na wspólnym okręgu – obliczenia polegają na znalezieniu jego promienia, a następnie podzieleniu przez niego promienia Ziemi. Szczegółowy opis wykorzystywanych w nim równań znajduje się na stronie Obliczenia.
Wysokości punktów na obu krańcach linii obserwacji są znane, odległość również – wysokości najlepiej odczytać na Geoportalu, zaś odległości zmierzyć na mapie Google lub policzyć jednym z kalkulatorów odległości online. Wysokość punktu na Górze Kamieńskiej wynosi ok. 403,4 m n.p.m. – dodając wysokość statywu przyjmijmy 405 m n.p.m., Łomnica ma 2634 m n.p.m., Lodowy Szczyt 2628 m n.p.m., a Gerlach 2655 m n.p.m. Pozostaje znaleźć punkt pośredni, czyli najdalszy punkt widoczny przed Tatrami na azymucie danego szczytu. Jego wyznaczenie składa się z kilku etapów. W tym celu za pomocą strony heywhatsthat.com tworzymy analizę widoczności dla tatrzańskiego szczytu (lub punktu obserwacji – nie ma to znaczenia) zgodnie z instrukcją, a następnie wyznaczamy położenie i wysokość szukanego punktu za pomocą tej metody.
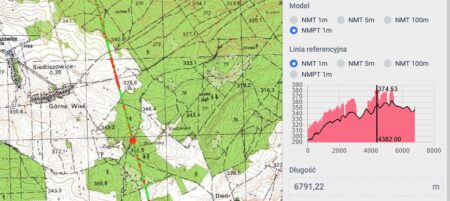
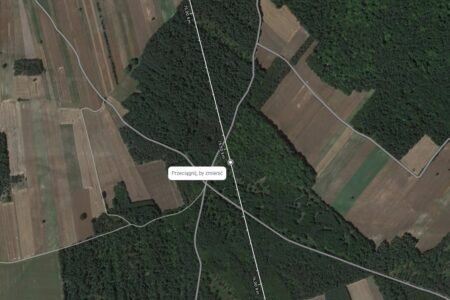
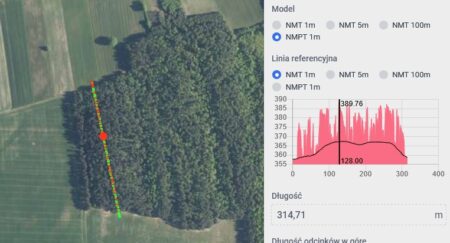
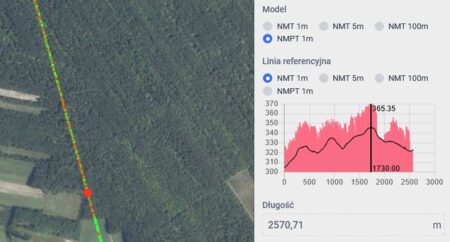
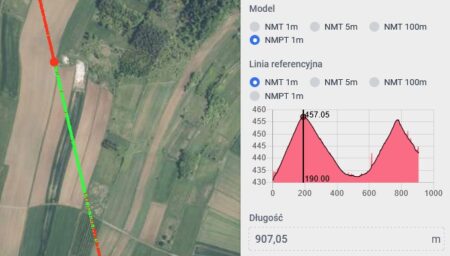
Poniższe ilustracje przedstawiają te pośrednie punkty na profilu z heywhatsthat.com (miejsce jest oznaczone pionową zieloną linią), na mapie z Geoportalu wraz z pomiarem wysokości modelem NMPT oraz na mapie Google z pomiarem odległości.
I tak w przypadku Tatr widzianych z Góry Kamieńskiej wygląda to następująco:
-
- Dla Łomnicy punkt pośredni znajduje się na wysokości ok. 380 m n.p.m., w odległości 75,55 km od Góry Kamieńskiej
- Dla Lodowego Szczytu wyznaczenie tego punktu jest trudniejsze – na mapie Google linia obserwacji jest nieco przesunięta względem Heywhatsthat i Geoportalu, potencjalny punkt wyznaczony na podstawie Heywhatsthat i Geoportalu to las, o który ledwo zahacza linia na mapie Google.
punkt 1 – 390 m n.p.m., 75,8 km
punkt 2 – 370 m n.p.m., 73,3 km
Na zdjęciu widać, że po lewej stronie szczytu horyzont jest wyżej niż po prawej – najprawdopodobniej las kończy się na tle góry. Punkt 1. jest zatem odpowiedni dla pomiaru wysokości względem horyzontu widocznego po lewej, natomiast punkt 2. – po prawej.

- Dla Łomnicy punkt pośredni znajduje się na wysokości ok. 380 m n.p.m., w odległości 75,55 km od Góry Kamieńskiej
- Dla Gerlacha punkt ten leży na wysokości 457 m n.p.m., w odległości ok. 86,8 km.
Wprowadzamy dane do arkusza kalkulacyjnego i otrzymujemy następujące wartości współczynnika refrakcji:
- dla Łomnicy 0,174
- dla Lodowego Szczytu i punktu 1. 0,178, dla punktu 2. 0,169
- dla Gerlacha 0,203
Przy takiej średniej refrakcji szczyty te byłyby widoczne dokładnie za wyznaczonymi punktami pośrednimi – równo z horyzontem, czyli… właściwie niewidoczne. Dopiero dalsze zwiększanie refrakcji spowodowałoby podniesienie obrazu szczytów ponad zasłaniający je teren.
Pomiar współczynnika refrakcji w chwili obserwacji na podstawie zdjęć
Analizując zdjęcia, można zmierzyć, jak bardzo refrakcja pozornie podniosła szczyty w górę, a także oszacować średni współczynnik refrakcji w momencie fotografowania.
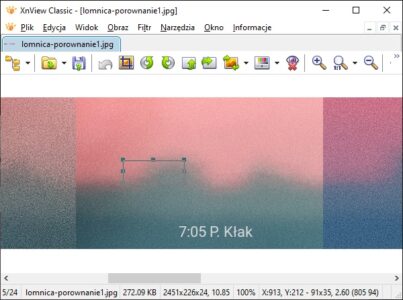
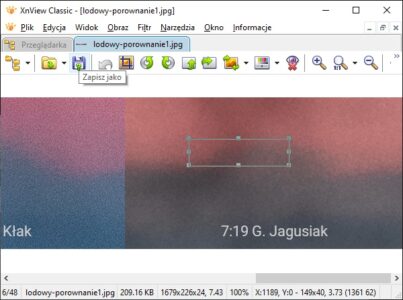
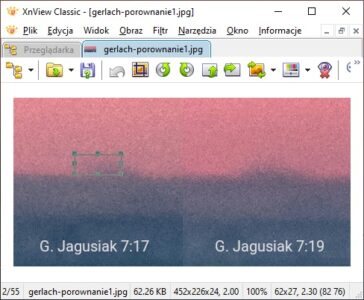
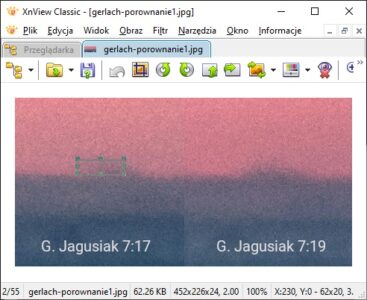
W tym celu zestawiłem zdjęcia wykonane co kilka minut, z dopasowaną wielkością, tak aby możliwe było porównanie wyglądu szczytów. Poziome linie przebiegające co 20 pikseli ułatwiają porównanie, jak wysoko wierzchołki wystają nad horyzont.
Należy teraz zmierzyć, jak wysoko szczyty wystają nad horyzontem. Taki pomiar umożliwia wiele programów graficznych, np. XnView, w którym najlepiej zrobić to, rysując zaznaczenie prostokątne na wysokość widocznej części góry. W dolnej części okna automatycznie pojawiają się wymiary zaznaczenia, z których drugi oznacza wysokość (wymiar pionowy).
Łomnica wystaje na ok. 35-59 pikseli. Pomiary są utrudnione ze względu na nieostrość obrazu, nie da się więc zrobić tego z idealną dokładnością. Orientacyjnie dokładność w tych warunkach można oszacować na ok. 10 pikseli.
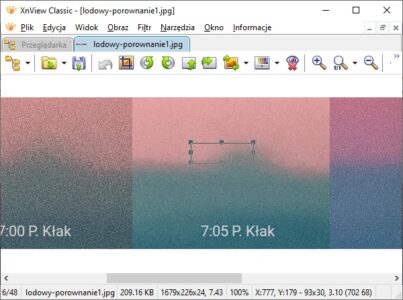
Lodowy Szczyt wystaje na ok. 30-40 pikseli względem horyzontu po jego lewej stronie.
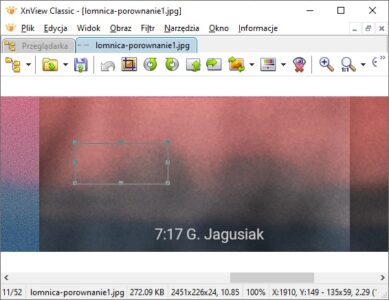
Gerlach wystaje na ok. 20-27 pikseli w zależności od tego, czy zmierzymy go razem ze słabo widocznym obszarem nieco ciemniejszym od nieba, który może odpowiadać rozmytemu fragmentowi szczytu. Pomiary Gerlacha były wykonane na zdjęciach w oryginalnym rozmiarze (bez dopasowywania do rozmiarów pozostałych zdjęć), wymagających oddzielnego wyznaczenia rozdzielczości.
Przeliczamy piksele na metry. Można to zrobić, obliczając kąt widzenia obiektywu o danej ogniskowej, jednak obiektywy typu zoom poza skrajnymi położeniami mogą niedokładnie podawać wartość ogniskowej. Dokładniejsze będzie obliczenie różnicy azymutów pomiędzy widocznymi szczytami i podzielenie przez nią wielkości poziomego odstępu między nimi na zdjęciu w pikselach.
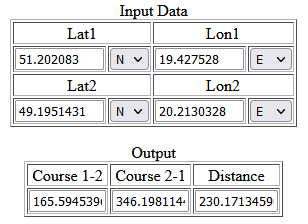
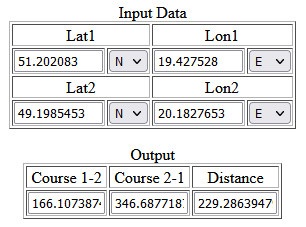
Azymuty można obliczyć, podając współrzędne punktów w kalkulatorze Eda Williamsa.
Różnica azymutów wynosi 0,5128°, po przeliczeniu na radiany 0,0089500484 rad. Na zdjęciu szczyty oddziela odstęp 950 pikseli. Dzielimy azymut (w radianach) przez ten odstęp – otrzymany wynik to rozdzielczość kątowa zdjęć.
0,0089500484 rad / 950 px ≈ 0,000009421 rad/px
Następnie mnożymy ją przez zmierzoną wcześniej wysokość widocznych części szczytów w pikselach i przez odległość do szczytu w metrach – uzyskujemy wysokość widocznych części gór.
Dla Łomnicy:
- 0,000009421 rad/px * 35 px * 230100 m ≈ 76 m
- 0,000009421 rad/px * 53 px * 230100 m ≈ 128 m
Dla Lodowego Szczytu:
- 0,000009421 rad/px * 30 px * 229200 m ≈ 65 m
- 0,000009421 rad/px * 40 px * 229200 m ≈ 86 m
Dla Gerlacha (rozdzielczość zdjęć wynosi 0,000013355 rad/px):
- 0,000013355 rad/px * 20 px * 232100 m ≈ 62 m
- 0,000013355 rad/px * 27 px * 232100 m ≈ 84 m
Teraz, aby policzyć współczynnik refrakcji i wysokość podniesienia obrazu szczytów przez refrakcję, musimy mieć punkt odniesienia, względem którego będziemy ją liczyć. Wracamy więc do wyznaczonych wcześniej punktów pośrednich.
Wartość średniego współczynnika refrakcji, jaki wystąpił w momencie obserwacji, liczymy analogicznie jak wyżej opisany minimalny współczynnik refrakcji, za pomocą tego samego arkusza, ale jako wysokość obserwowanego obiektu wpisujemy różnicę wysokości szczytu i widocznego fragmentu góry. Przykładowo dla obserwacji Gerlacha na zdjęciu Pawła jest to 2655 – 62 = 2593 m n.p.m.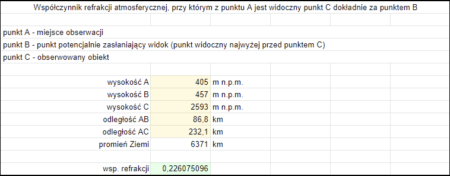
Otrzymujemy następujące wyniki:
- Łomnica 0,202 – 0,22
- Lodowy Szczyt 0,202 – 0,209
- Gerlach 0,226 – 0,234
Największa refrakcja wystąpiła ok. godz. 7:17 – ok. 0,22 dla Łomnicy i (po uśrednieniu) ok. 0,23 dla Gerlacha, choć dla Lodowego Szczytu wyszło nieco mniej (0,209). Na zdjęciu, na którym Gerlach jest najlepiej widoczny, Lodowy Szczyt jest w znacznej części zasłonięty gałęziami, co uniemożliwia miarodajny pomiar. Ponadto rozbieżności wynikają przede wszystkim z niejednorodności refrakcji – jej zmienności w czasie i przestrzeni, nieostrości obrazu na zdjęciach, a także obecności gałęzi, które w niektórych miejscach zlewały się z górami, utrudniając pomiary.
Obliczenie wysokości refrakcyjnego podniesienia szczytów
Tutaj również przyda się arkusz kalkulacyjny – jego część zatytułowana „Wysokość pozornego podniesienia obiektu pod wpływem refrakcji na podstawie zdjęcia”. Zawarte w nim formuły wyznaczają minimalną wysokość szczytu, jaką musiałby mieć, aby był widoczny przy standardowej refrakcji (poprzez wyznaczenie wysokości punktu leżącego na okręgu wspólnym dla punktu obserwacji i punktu pośredniego, o promieniu równym promieniowi Ziemi podzielonemu przez standardowy współczynnik refrakcji 0,13), a następnie jest od niej odejmowana rzeczywista wysokość wierzchołka i dodawana wysokość widocznej części góry.
W ten sposób otrzymujemy wysokość, o jaką szczyty został musiałyby być wyższe, aby w standardowych warunkach były widoczne tak, jak przy zwiększonej refrakcji atmosferycznej.
Po wprowadzeniu obliczonych powyżej wysokości widocznych części szczytów oraz pozostałych niezbędnych danych, otrzymujemy następujące wartości:
- Łomnica 200 – 252 m
- Lodowy Szczyt 198 – 219 m
- Gerlach 255 – 277 m
Wysokość podniesienia obserwatora odpowiadająca efektowi działania refrakcji
Refrakcja atmosferyczna daje nieco podobny efekt, jaki uzyskamy, wznosząc się w górę – zarówno w jednym, jak i drugim przypadku widok obejmuje większą odległość, a dalsze obiekty wystają wyżej ponad bliższymi. Występują jednak znaczne różnice w geometrii takiego widoku – działanie refrakcji zwiększa się z odległością, natomiast tutaj jest odwrotnie – im bliżej, tym kolejne plany panoramy bardziej oddalają się wizualnie od siebie. Dlatego zwiększenie wysokości obserwatora daje efekt równoważny refrakcji tylko w odniesieniu do punktu leżącego w określonej odległości od obserwatora – czyli w naszym przypadku względem wyznaczonych powyżej punktów na horyzoncie, ponad którymi wystają tatrzańskie wierzchołki. Szersze omówienie tematu znajduje się w tekście o refrakcji w symulacjach widoczności.
Możemy więc obliczyć wysokość, na którą należałoby się wznieść ponad Górę Kamieńską, aby przy standardowej refrakcji góry wystawały nad horyzontem o taką samą wysokość, jak w przypadku niniejszej obserwacji ze zwiększoną refrakcją. Wykorzystamy tu ten sam arkusz kalkulacyjny – część „Pozorne podniesienie obserwowanego punktu pod wpływem wzrostu refrakcji atmosferycznej”.
Wyniki są następujące:
- dla Łomnicy 98 – 123 m
- dla Lodowego Szczytu 98 – 108 m
- dla Gerlacha 152 – 165 m
Znajdujące się na Górze Kamieńskiej turbiny wiatrowe mają całkowitą wysokość 121 m – z końcówek ich łopat w najwyższym położeniu wierzchołki Łomnicy czy Lodowego Szczytu byłyby widoczne przy standardowej refrakcji, co oznacza, że również z tych szczytów można byłoby dostrzec turbiny. Byłoby to jednak trudne, gdyż cienkie łopaty są o wiele mniejsze i przez to trudniejsze do zauważenia niż szczyty gór. Nawet niewielkie rozmycie obrazu przez niejednorodne załamanie światła w powietrzu mogłoby całkowicie zatrzeć ich zarysy.














Bardzo dobra analiza!
[…] You can find a full report on the dalekiewidoki.pl website. Calculations of refraction for this observation can be found in an article on Dalekie Horyzonty. […]