poświęcony wyznaczaniu odległości obserwacji zainspirował mnie do spojrzenia na nie w nowym świetle, by zilustrować rozbieżności w wynikach opracowań przygotowanych różnymi narzędziami i być może zrobić krok w stronę rozwiązania tego problemu.
Jeśli porównać opisy na stronie dalekiewidoki (zrobiony przez Pawła i mój), to nie sposób nie zauważyć, że odległość od Kalenicy do Babiej Góry różni się na nich o przeszło pół kilometra. Podobnie było w wielu innych przypadkach – otrzymywałem odległości mniejsze, niż koledzy analizujący tę samą obserwację. Kładłem to dotąd na karb tego, że „idę na łatwiznę” i wyznaczam odległość jako długość odcinka łączącego 2 punkty, nie biorąc pod uwagę krzywizny linii widzenia, a już na pewno nie krzywizny powierzchni Ziemi. Uważałem bowiem i nadal uważam, że przy obliczaniu odległości między punktami najlepiej trzymać się najprostszego sposobu, zamiast wikłać w uwzględnianie refrakcji, która powoduje, że długość linii widzenia (czyli drogi punktu na froncie fali) zmienia się w zależności od warunków termicznych, a jeśli pojawiają się miraże, to jest więcej niż jedna taka linia. O tym, że światło nie mknie po powierzchni Ziemi, chyba nie trzeba przekonywać :-). W obliczeniach omówionych w artykule Łukasza zostało zresztą jasno pokazane, że wszelkie krzywizny wnoszą stosunkowo niewiele, a już na pewno nie wspomniane pół kilometra z okładem. Jeśli dobrze przemyśleć ten aspekt sprawy, to jest on do rozwiązania (zgrubnego, lecz wystarczającego) na poziomie szkolnej geometrii – wystarczy porównać długość cięciwy i łuku okręgu.
Jeśli nie krzywizna, to co powoduje tak duże różnice? Podejrzanie padło na parametry elipsoidy przybliżającej kształt Ziemi. W swoich obliczeniach stosowałem „starą” elipsoidę Krasowskiego, podczas gdy w powszechnym użytku jest obecnie WGS-84. Nie ma sensu wdawać się w dywagacje, która z nich lepiej sprawdza się na obszarze Polski – zmiana parametrów w programie jest trywialna, a porównywać chcemy wyniki otrzymane z tą samą elipsoidą. Zmiana taka powoduje znaczące przesunięcie współrzędnych kartezjańskich punktu o danych współrzędnych geograficznych, ale odległość pomiędzy dwoma punktami znajdującymi się około 200 km od siebie zmienia się zaledwie o kilka metrów. Jest ona znacznie mniejsza od rozmiarów Ziemi, a oba punkty przesuwają się podobnie, gdy zmieniamy elipsoidę. Wyjaśnienia kilkusetmetrowych różnic nadal brakowało.
Przysłowiowe szydło wyszło z worka dopiero w dyskusji, w której okazało się, że internetowe kalkulatory do obliczeń odległości traktują odczytane z map współrzędne nie jako geograficzne, lecz geodezyjne! O tych pierwszych każdy przynajmniej słyszał w szkole, o drugich – niekoniecznie.
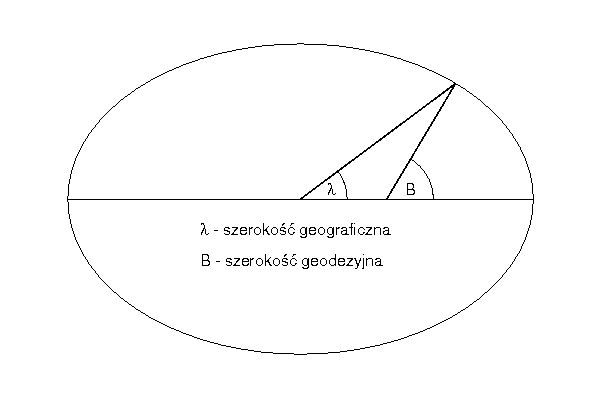
Różnica dotyczy szerokości – geograficzna jest kątem pomiędzy płaszczyzną równikową i prostą przechodzącą przez dany punkt oraz środek Ziemi, natomiast geodezyjna kątem pomiędzy tą samą płaszczyzną i normalną do powierzchni elipsoidy ziemskiej. Pierwsza jest uniwersalna – można ją wyznaczyć na podstawie precyzyjnych obserwacji astronomicznych. Druga zależy od parametrów elipsoidy, ale za to punkty ustawione jeden nad drugim (dokładnie w pionie) mają taką samą szerokość geodezyjną. Jeśli kształt Ziemi przybliżamy kulą (model FAI w artykule Łukasza), to współrzędne geodezyjne stają się tożsame z geograficznymi.
Czas przejść do obserwacji. Pokazane zdjęcia, a właściwie składanki dwóch lub trzech kadrów pokazują ewolucję widoku Beskidów w ciągu niemal godziny. Do dwóch przygotowałem opisy w obu wariantach, ze współrzędnymi traktowanymi na dwa sposoby. Odległości, podane w nawiasach, są zaokrąglone do 100 m. Tu trzeba nadmienić, że szerokość geodezyjna każdego punktu na obszarze Polski jest o około 10 minut kątowych większa od jego szerokości geograficznej, z dowolną rozsądną elipsoidą. Ma to swoje konsekwencje. Z map odczytujemy współrzędne kątowe i jeśli zinterpretujemy je jako geodezyjne, to obliczone odległości między punktami – zwłaszcza w kierunkach zbliżonych do równoleżnikowych – są większe, niż gdybyśmy potraktowali te same współrzędne jako geograficzne. Dzieje się tak dlatego, że nasze punkty (oczywiście tylko w obliczeniach, bo w rzeczywistości są tam, gdzie są względem środka Ziemi) znajdą się bliżej płaszczyzny równikowej, a przekrój Ziemi płaszczyzną równoległą do równikowej ma coraz większy obwód w miarę zbliżania się do równika. Z tego samego powodu o kilka minut różnią się wyznaczone kąty azymutu.
Zaczynamy około pół godziny przed wschodem Słońca, o 7:20. Jest jeszcze dość ciemno, a na wielu masztach i wiatrakach (DH1 i DH2 koło Dívčí Hradu) są włączone światła sygnalizacyjne, dzięki którym można dobrze dopasować symulację do zdjęć. Ta sztuka udaje się z obydwoma rodzajami współrzędnych.
Najdalej widać wypłaszczenie Kępy we wschodnim grzbiecie Babiej Góry. Tu też występuje największa rozbieżność obliczonej odległości – we współrzędnych interpretowanych jako geograficzne wynosi ona 244,8 km, a jako geodezyjne – 245,6 km. Około 800 metrów różnicy. Maleje ona dla bliższych obiektów – np. w przypadku Skrzycznego wynosi około 700 m (206,3 versus 207,0 km), szczytów Gór Opawskich – około 300 m przy około 80 km odległości, a zamku-pałacu Marianny Orańskiej w Kamieńcu Ząbkowickim – zaledwie około 100 m (27,2 i 27,3 km). Mamy do czynienia ze skalowaniem obliczonego dystansu czynnikiem 1,0033.
Charakterystyczne spłaszczenie optyczne odległych gór, związane z silnym uginaniem światła rozchodzącego się w warstwie powietrza z największą inwersją temperatury, w której występuje anomalnie wysoki gradient współczynnika załamania światła, doskonale widać na przykładzie masywu Babiej Góry oraz pasma Klimczoka, które wydają się niemal pozbawione przewyższeń. Takich warstw leżących jedna nad drugą można wskazać więcej, w postaci ciemniejszych pasów. W jednej z nich nad Skrzycznem powstał odwrócony miraż nakładający się na obraz zwyczajny. Ponadto widać, jak dalekie góry chowają się za krzywizną Ziemi – wyższa o ponad 600 m i odleglejsza o ponad 40 km Babia Góra jest pozornie tak samo wysoko, jak Klimczok.
Dwanaście minut później, o 7:32 robi się już znacznie jaśniej. Gaśnie większość świateł sygnalizacyjnych. Obserwowany fragment Babiej Góry kurczy się do samej kopuły szczytowej, najokazalszym mirażem staje się nieduża „wieżyczka z działkiem” nad szczytem Klimczoka, a koło szczytu Skrzycznego daje się zauważyć maszt RTON.
Po upływie kolejnych 17 minut, o 7:49, czyli tuż przed wschodem Słońca, można wreszcie odróżnić od tła Muflon i Dębową Górę, na końcu Lasu Trzebińskiego – najodleglejszej od Gór Sowich części Gór Opawskich. W typowych warunkach termicznych zamykają one horyzont, natomiast w panującej inwersji widać za nimi pozbawiony wyraźniejszych wzniesień fragment terenu. Symulacja komputerowa z dostępnymi danymi nie potrafiła go pokazać (rzeczywiste warunki termiczne musiały różnić się od wyników nocnego pomiaru z Prostejova), ale musi się on znajdować około 10 km dalej (czyli około 95 km od obserwatora), po drugiej stronie rzeczki Osoblahy, między granicą państwa i Głubczycami. Miraże nad Beskidem Śląskim powiększają się, natomiast Babia Góra coraz mniej wystaje nad mgłę. Kontrast Beskidów na tle nieba wciąż pozostaje bardzo dobry. Ta panorama jest najszersza, więc należał się jej opis. Usunąłem z niego maszty, których już nie było widać i dodałem nowe obiekty, poprzednio pozostające poza kadrem.
Na wiatraku U3 w Unikowicach koło Paczkowa świeci ostatnie światełko. Nad Paczkowem dominuje wysoka wieża kościelna, a sam Paczków znalazł się prawie u stóp Skrzycznego – czy to nie piękny widok :-)?
Słońce wschodzi, ale dla obserwatora na Kalenicy pozostaje schowane za Jesionikami i jeszcze nie zalewa blaskiem leżącej na przedpolu doliny Nysy Kłodzkiej. Oświetla za to mgły rozpościerające się za górami i kontrast trochę się pogarsza. O 7:58 Beskidy są jednak nadal wyraźnie widoczne, a nad Beskidem Śląskim tworzą się coraz okazalsze miraże. Na tym zdjęciu, a także na ostatnim, zrobionym już w pełnym świetle o 8:10, po lewej stronie panoramy daje się zauważyć pojedynczy wiatrak.
Musi być stosunkowo nowy, bo nie ma go jeszcze na mapach. Na pewno nie jest to wiatrak w Zawiszycach koło Głubczyc – nie zgadza się azymut. Czekam na podpowiedzi :-).
Beskidy było jeszcze widać przez kilkanaście minut. Ich obserwacja stawała się coraz trudniejsza i nie pomagało nawet wypiętrzenie optyczne silniejsze, niż przez poprzedzające pół godziny (Babia Góra znowu pokazała się aż do Gówniaka), ponieważ słabł kontrast na tle nieba. Klimczok pozornie lewitował nad mgłami… Coraz częściej patrzyłem więc w innych kierunkach, które z kolei stawały się atrakcyjniejsze w świetle słonecznym. O 8:30 spotkała mnie przy tym niespodzianka. Za Wzgórzami Lewińskimi, na prawo od Gór Orlickich, w obniżeniu między Skutiną i Grodczynem pojawiło się… coś.
Niczego się tam nie spodziewałem i nie miałem pojęcia, co widzę, ale od czego jest aparat fotograficzny :-)? Analiza zdjęcia przyniosła odpowiedź – to była góra Vestec (668 m n.p.m.) w Železnych horach, stanowiących część Wyżyny Czesko-Morawskiej. Niby tylko 113 km, ale zawsze to coś :-).
Warto zwrócić uwagę na opisy – różnica między współrzędnymi geograficznymi i geodezyjnymi staje się mniejsza w kierunku bardziej południkowym. Przy tej odległości wyniosła ona około 200 m, czyli mniej niż przy 80 km w kierunku Gór Opawskich. Zdziwiło mnie trochę, że góry we współrzędnych geodezyjnych „siadły”, tzn. ich obliczone pozycje są znacznie niżej, niż rzeczywiste, ale zapewne wynika to z nieadekwatnego pionowego profilu temperatury. Od pomiaru minął już szmat czasu. Zaskakująca jest jednak duża zmiana wyników w stosunku do obliczeń we współrzędnych geograficznych.
W podsumowaniu chciałoby się napisać, jakie właściwie współrzędne odczytujemy z map – geograficzne czy geodezyjne? Niestety nie potrafię jednoznacznie odpowiedzieć. Internetowe serwisy mapowe (geoportal, mapy.cz, mapy Google) generalnie zgadzają się między sobą. O różnicach 10 minut kątowych nie ma mowy. Możemy zatem bezpiecznie przyjąć, że wszystkie stosują ten sam rodzaj współrzędnych. Jeśli chodzi o ustalenie ich rodzaju, to wszystkie instrukcje „dla ludności” mówią o współrzędnych geograficznych. Wydawałoby się, że sprawa jest wyjaśniona, ale nie ma tak dobrze. Czy autorzy kalkulatorów odległości dysponują jakąś tajemną wiedzą, czy się mylą? Ziarno niepewności zasiewają oznaczenia szerokości i długości, odczytywanych na geoportalu: B i L, używane zwyczajowo dla współrzędnych geodezyjnych, w dodatku z podaną elipsoidą – nieodzowną dla nich! Żeby jeszcze bardziej sprawę zaciemnić, na tymże geoportalu można nałożyć na mapę siatkę nazywaną wprost geograficzną, z symbolami lambda i fi. Siatka ta doskonale zgadza się z odczytywanymi dla wybranego punktu liczbami. Napisałem na adres kontaktowy geoportalu pytanie połączone z prośbą o wyjaśnienie tej sprzeczności. Pozostaje bez odpowiedzi już od miesiąca. Co jakiś czas szukam dalej i jedyne, co znajduję, to narastającą niepewność. Najpiękniejszy kwiatek rośnie na geoforum. Pozwolę sobie zacytować fragment tekstu, autorstwa pani profesor Krystyny Podlachy.
„W roku 1987 JAG oraz Komisja VIII CERCO (Comite Europeen de Responsables de la Cartographic Officielle) powołały specjalną komisję i grupę roboczą, które w ścisłej współpracy podjęły badania i rozwinęły prace organizacyjne nad nowym Europejskim Systemem Odniesienia – ETRS (European Terrestrial System). W pierwszej kolejności kampaniami pomiarowymi (1988 r.) objęto kraje Europy Zachodniej. Wyniki pomiarów poddane zostały wstępnej obróbce, a następnie obliczono całą sieć i ustalono ostateczny wykaz współrzędnych ETRF-89. ETRF-89 wyrażony jest w układzie współrzędnych geograficznych geodezyjnych.”
Na widok nazwy „współrzędne geograficzne geodezyjne” opadły mi ręce. Dla człowieka spoza branży, nie rozumiejącego żargonu geodezji i kartografii – zapewne oczywistego dla specjalistów – nazwa ta brzmi tak samo logicznie, jak współrzędne sferyczne kartezjańskie, albo – żeby użyć języka zrozumiałego także dla dzieci – kwadratowe koło. Współrzędne geograficzne mają sens geometryczny inny, niż geodezyjne! Nie wiadomo, czy chodzi o użycie współrzędnych geodezyjnych w roli geograficznych, czy geograficznych w geodezji. Mówią: geograficzne, myślą: geodezyjne, a może na odwrót? Odnoszę wrażenie, że idziemy drogą wytyczoną przez radzieckiego generała Kudriawcewa, domagającego się fałszowania map (faktycznie robiono to w czasach słusznie minionych), bo najważniejsze są koordynaty, a jeśli wróg nie będzie ich znał, to jego pociski nie trafią w cele. Teraz mapy nie są już fałszowane, w internetowych serwisach wszystko można z nich odczytać, ale co z tego, skoro nawet najprzebieglejszy diabeł nie będzie wiedział, jakie współrzędne odczytał, jeśli nie zrobił doktoratu z geodezji i kartografii. Dlatego bardzo proszę – jeśli ten artykuł przeczyta ktoś, kto może wyjaśnić w sposób autorytatywny i bez zagadek godnych Sfinksa, najlepiej z podaniem źródła informacji, jakie współrzędne są tam stosowane – niech to zrobi. Będzie miał zagwarantowaną moją wdzięczność.
Bez tego nasze obliczenia odległości obserwacji pozostaną obarczone poważną niepewnością – tym większą, im dalej coś dostrzeżemy.
Krzysztof Strasburger
Jeszcze raz gratulacje za grudniową, świetnie opisaną obserwację! Dopiero czytając papierowy artykuł w „Sudetach”, uświadomiłem sobie, jak dużą część Babiej Góry było wtedy widać, nie tylko sam wierzchołek (niesamowite).
I kwestia druga — myślałem, że w tym temacie już wszystko powiedziano, a tu proszę, kolejne ciekawe rozważania i dobrze, że ten wpis się pojawił. Choć w temacie współrzędnych zrobiło się jeszcze wieksze zagmatwanie, to przynajmniej wiem już, czym różnią się współrzędne geograficzne od geodezyjnych 😉