Określenie odległości do widocznych w oddali obiektów wydają się proste, zwłaszcza, że jest podawana automatycznie przez popularne programy wspomagające identyfikację widoków. W gruncie rzeczy jest to prawda, pod warunkiem, że nie wymagamy dużej dokładności. Porównując dystanse obliczone w różnych programach, czy też podane na zdjęciach różnych autorów, można zauważyć, że nie są one identyczne. Rozbieżności te są wynoszą zazwyczaj kilkaset metrów, lecz mogą być większe i wynikają między innymi z różnych sposobów obliczeń.

Oto możliwe główne przyczyny tych różnic.

1. Model kształtu Ziemi. Ziemia ma kształt geoidy – nieregularnej bryły, najbardziej zbliżonej do elipsoidy obrotowej. Niektóre programy wykonują obliczenia dla elipsoidy (najczęściej WGS 84), natomiast te najczęściej używane wykorzystują uproszczony model idealnej kuli – tzw. model FAI o promieniu 6371 km, obarczając wyniki niewielkim błędem. Różnice między geoidą a elipsoidą WGS 84 są pomijalnie małe (maksymalnie do 100 metrów w pionie), natomiast pomiędzy modelami WGS 84 a FAI sięgają ponad 14 km w pionie. W kierunku północ-południe model FAI zawyża odległość na małych szerokościach geograficznych (poniżej ok. 48°), natomiast na większych zaniża. W kierunku wschód-zachód odległości w tym modelu są zawsze zaniżane. Z tego względu na terenie Polski odległości w modelu FAI są zaniżone:
   • w kierunku równoleżnikowym ok. 300 m na dystansie 100 km,
   • w kierunku południkowym – od ok. 20 m na 100 km na południu Polski do ok. 100 m na 100 km w Polsce północnej.
2. Dystans w linii prostej lub po obwodzie Ziemi. Dla odległości, na które jest możliwy widok na Ziemi, różnice są dość małe (ok. 8 m dla 200 km, 128 m dla 500 km).
3. Uwzględnianie wysokości n.p.m. Punkty położone na dużej wysokości są od siebie bardziej oddalone niż gdyby znajdowały się na poziomie morza. Niektóre generatory panoram nie biorą pod uwagę wysokości w obliczeniach. W wysokich górach skutkuje to błędem mogącym przekraczać 100 m na 100 km.
4. Błąd określenia lokalizacji punktów. Może wynikać np. z niedokładnie podanego położenia obserwatora czy błędów modelu terenu na symulacji panoramy.
5. Nietypowe metody zaokrąglania liczb. Takim przykładem jest zaokrąglanie do połówek kilometrów (zamiast np. do liczby całkowitej lub 0,1 km), które ze względu na obecność cyfry po przecinku sugeruje, że dokładność wynosi 0,1 km. Maksymalny możliwy błąd wynosi w tym przypadku 0,25 km.
6. Pomiar odległości po drogach. Zdarza się, że niektórzy podają dystans w ten sposób, a jest to potencjalne źródło największych błędów. Dystans, jaki można byłoby pokonać drogami, jest znacznie większy niż w linii prostej i zależny od wybranej trasy (którą można dowolnie wydłużać). Często nie da się pokonać drogi do widocznego obiektu żadnym pojazdem, np. na strome górskie szczyty.

Metody obliczeń

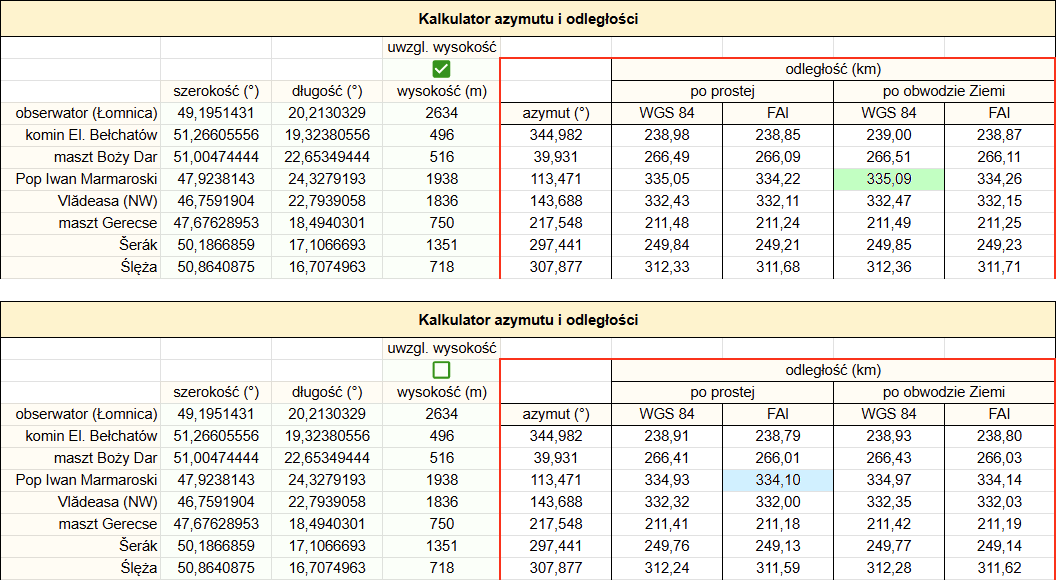
Jak już zostało wspomniane powyżej, odległość można liczyć według różnych modeli Ziemi, w linii prostej lub po obwodzie planety, z uwzględnieniem wysokości lub bez. W celu porównania metod przygotowałem arkusz kalkulacyjny, który po wpisaniu współrzędnych geograficznych i wysokości podaje odległość obliczoną na 8 sposobów – według modelu elipsoidalnego WGS 84 oraz kulistego FAI, w linii prostej lub po obwodzie Ziemi i wszystkie te 4 metody z uwzględnieniem wysokości lub bez. Za jego pomocą można sprawdzić, jaka metoda jest stosowana w danym programie.

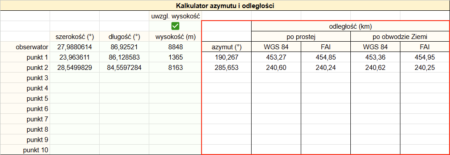
Najdokładniejsza jest metoda po linii prostej na elipsoidzie WGS 84, z uwzględnieniem wysokości – otrzymujemy rzeczywisty dystans pomiędzy dwoma punktami, a potencjalny błąd wynikający z różnic między elipsoidą a geoidą jest minimalny. Obliczenia nie zawierają żadnych innych uproszczeń. Współrzędne geograficzne (w zasadzie geodezyjne) są przeliczane na kartezjańskie w przestrzeni, a te na odległość.
W analogiczny sposób wykonywane są obliczenia dla modelu FAI – współrzędne są liczone dla kuli o promieniu 6371 km.
Dla dystansu wzdłuż krzywizny Ziemi obliczenia są nieco inne. W modelu FAI na poziomie morza są dość proste i możliwe na kilka sposobów, dających identyczny wynik. Można np. przeliczyć odległość w linii prostej na odległość sferyczną po obwodzie Ziemi wzorem

gdzie l – odległość sferyczna, d – dystans w linii prostej, r – promień Ziemi (6371 km). Trudniej jest w modelu WGS 84 – precyzyjne obliczenia na elipsoidzie przy użyciu wzorów Vincentego są bardzo skomplikowane, iteracyjne. Z tego powodu w arkuszu przyjąłem uproszczoną metodę, dodając do odległości w linii prostej wg WGS 84 różnicę pomiędzy odległością sferyczną i prostoliniową wg modelu FAI. Dokładną wartość bez uproszczeń można uzyskać kalkulatorem online Eda Williamsa, różnice są jednak minimalne, rzędu centymetrów.
Czy można wykonać analogiczne obliczenia z uwzględnieniem wysokości punktów nad poziomem morza? Najprościej można powiedzieć – i tak, i nie. Jeśli punkty są położone na identycznej wysokości, wtedy można po prostu zwiększyć promień Ziemi o tę wysokość i otrzymamy odległość po okręgu równoległym do poziomu morza. Sytuacja komplikuje się dla punktów położonych na różnych wysokościach. Nie da się wtedy wyznaczyć okręgu ani elipsy równoległej do poziomu morza, przechodzącego przez oba te punkty. Można co najwyżej określić podobną, przybliżoną figurę geometryczną. W arkuszu przyjąłem następujący sposób dla modelu FAI – okrąg przechodzący przez oba punkty, o promieniu równym sumie promienia Ziemi (6371 km) i średniej arytmetycznej wysokości bezwzględnych tych punktów. Z kolei dla WGS 84, podobnie jak dla poziomu morza, do odległości w linii prostej jest dodawana różnica między odległościami po ww. okręgu i linii prostej w modelu FAI.
Azymut jest zawsze liczony najprostszą metodą – w modelu FAI na poziomie morza.

 

Porównanie pomiarów odległości najpopularniejszymi narzędziami internetowymi

Mount Everest: 27,9880614°N 86,92521°E, 8848 m n.p.m.
Parasnath Hills: 23,963611°N 86,128583°E, 1365 m n.p.m.
Manaslu: 28,5499829°N 84,5597284°E, 8163 m n.p.m.

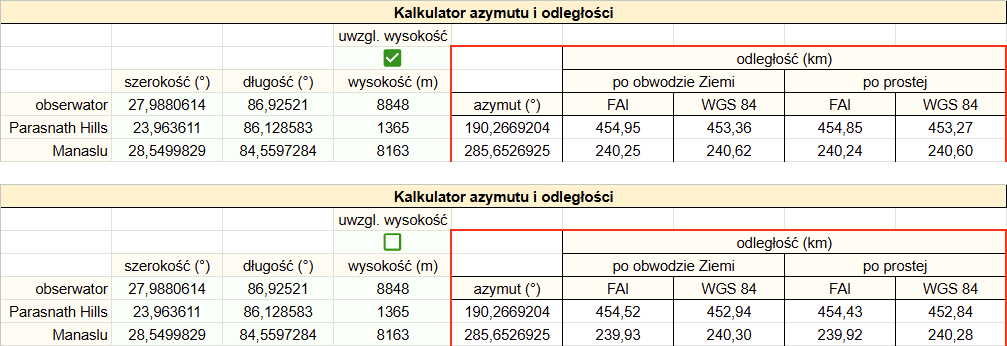
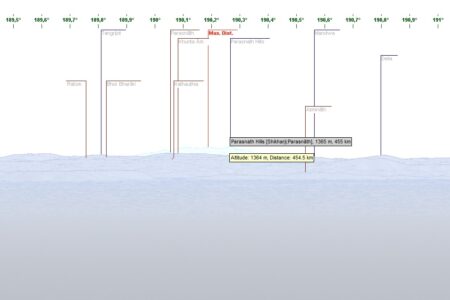
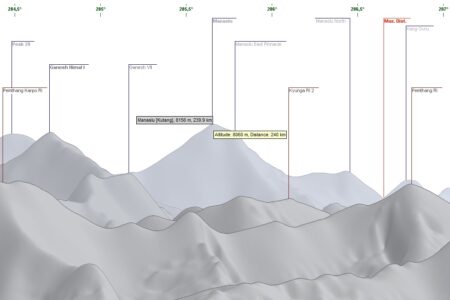
Zgodnie z teoretycznymi przewidywaniami, na małej szerokości geograficznej (poniżej 48°) model FAI zawyża odległość w kierunku zbliżonym do południkowego (do Parasnath Hills – azymut 190°), natomiast zaniża w kierunku bliskim równoleżnikowemu (do Manaslu – azymut 286°). Dla Parasnath Hills różnice pomiędzy metodami sięgają ponad 2 km.

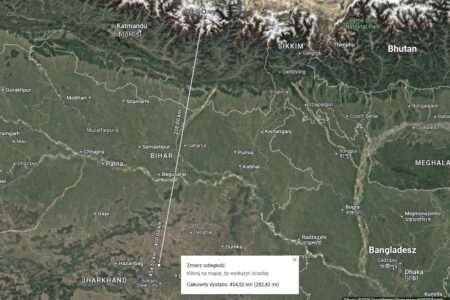
Mapy Google

Odległość do Parasnath Hills to 454,52 km, do Manaslu 239,93 km. Oznacza to, że są one obliczone według modelu FAI (kula o promieniu 6371 km), wzdłuż obwodu Ziemi i nie uwzględniają wysokości n.p.m. Błąd tej metody może wynosić ok. 0,5%.

Generator panoram udeuschle.de

Odległość do Parasnath Hills to 454,5 km, do Manaslu 239,9 km. Podobnie jak na Mapach Google, są obliczone dla modelu FAI (kula o promieniu 6371 km), wzdłuż obwodu Ziemi i nie uwzględniają wysokości n.p.m. Błąd tej metody może wynosić ok. 0,5%.

Peakfinder

Kalkulator Eda Williamsa

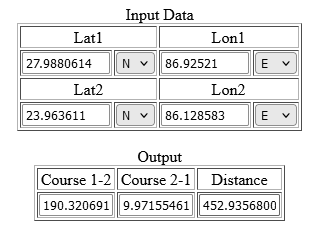
Porównanie odległości dla Tatr

Podsumowanie

Którą metodę najlepiej wybrać? Najdokładniejsza jest według elipsoidy WGS 84, w linii prostej, z uwzględnieniem wysokości. Prawdopodobnie jest wykorzystywana przez Peakfinder, ale ze względu na możliwe niedokładności modelu terenu, ograniczony zasięg i brak niektórych obiektów najlepiej skorzystać z arkusza kalkulacyjnego. Mapy Google i generator panoram Ulricha Deuschle używają mniej dokładnego modelu FAI i nie uwzględniają wysokości, dlatego odległości są obarczone błędem, który może wynosić do ok. 0,5%.