Obliczenia

Obliczenia wykorzystywane w arkuszach kalkulacyjnych.

Spis treści

Arkusz 3. – refrakcja atmosferyczna

Arkusz 4. – kąt widzenia obiektywu i powiększenie obrazu

 

Arkusz 3. – refrakcja atmosferyczna

Współczynnik refrakcji wymagany do widoczności obiektu

 

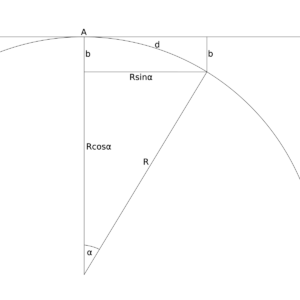
Przy stałym współczynniku refrakcji światło przebiega po okręgu. Jeśli z punktu A punkt C jest widoczny dokładnie za punktem B, oznacza to, że wszystkie te trzy punkty należą do okręgu, po którym światło biegnie pomiędzy nimi.
Współczynnik refrakcji jest zatem obliczany jako iloraz promienia Ziemi i promienia okręgu, na którym znajdują się punkty A, B i C. Obliczenia promienia tego okręgu są wykonywane przy założeniu kulistego kształtu Ziemi, w układzie współrzędnych kartezjańskich, gdzie środek Ziemi ma współrzędne (0,0), natomiast xA=0.

Oznaczenia:

  • hA, hB, hC – wysokości n.p.m. punktów A, B, C (m)
  • dAB, dAC – odległości pomiędzy punktami A i B oraz A i C, mierzone wzdłuż powierzchni Ziemi (po łuku, w km)
  • R – promień Ziemi (km)
  • xA, yA, xB, yB, xC, yC – współrzędne punktów A, B i C
  • x0, y0 – współrzędne środka okręgu, na którym znajdują się punkty A, B i C
  • r – promień okręgu, na którym znajdują się punkty A, B i C (km)
  • k – współczynnik refrakcji

Wartości hA, hB, hC, dAB, dAC, R są znane.

1. Wyznaczenie współrzędnych punktów A, B, C:

x_A=0\\ y_A=R+h_A\\ x_B=(R+h_B)\cdot\sin(d_{AB}/R)\\ y_B=(R+h_B)\cdot\cos(d_{AB}/R)\\ x_C=(R+h_C)\cdot\sin(d_{AC}/R)\\ y_C=(R+h_C)\cdot\cos(d_{AC}/R)

2. Podstawiając współrzędne punktów A, B, C do równania okręgu, otrzymujemy układ równań:
\begin{cases} (x_A-x_0)^2+(y_A-y_0)^2=r^2\\ (x_B-x_0)^2+(y_B-y_0)^2=r^2\\ (x_C-x_0)^2+(y_C-y_0)^2=r^2 \end{cases}

3. Po przekształceniu powyższych równań otrzymujemy:
\begin{cases} x_0=\dfrac{x_B^2+y_B^2-x_A^2-y_A^2+2y_0(y_A-y_B)}{2(x_B-x_A)}\\ y_0=\dfrac{x_C^2+y_C^2-x_A^2-y_A^2-2x_0(x_C-x_A)}{2(y_C-y_A)} \end{cases}\\ \\ y_0=\dfrac{x_C^2+y_C^2-x_A^2-y_A^2-\frac{(x_B^2+y_B^2-x_A^2-y_A^2)(x_C-x_A)}{x_B-x_A}}{2y_C-2y_A+\frac{2(y_A-y_B)(x_C-x_A)}{x_B-x_A}}
a następnie wyznaczamy x0 po podstawieniu y0:
x_0=\dfrac{x_B^2+y_B^2-x_A^2-y_A^2+2y_0(y_A-y_B)}{2(x_B-x_A)}=\dfrac{x_B^2+y_B^2-x_A^2-y_A^2+2(y_A-y_B)\frac{x_C^2+y_C^2-x_A^2-y_A^2-\frac{(x_B^2+y_B^2-x_A^2-y_A^2)(x_C-x_A)}{x_B-x_A}}{2y_C-2y_A+\frac{2(y_A-y_B)(x_C-x_A)}{x_B-x_A}}}{2(x_B-x_A)}
4. Wracamy do równania okręgu – liczymy promień okręgu, podstawiając x0 i y0:
(x_A-x_0)^2+(y_A-y_0)^2=r^2\\\\ r=\sqrt{(x_A-x_0)^2+(y_A-y_0)^2}

5. Współczynnik refrakcji wynosi:
k=\dfrac{R}{r},
lecz przyjmuje wartość ujemną, jeśli punkt B znajduje się poniżej prostej przechodzącej przez punkty A i C, czyli wtedy, gdy yB jest mniejsze od:
\dfrac{x_B(y_C-y_A)}{x_C}+y_A

Ujemna wartość k oznacza, że wypukłość krzywizny jest skierowana w kierunku Ziemi.

 

Podniesienie obserwowanego punktu pod wpływem refrakcji o znanym współczynniku

Oznaczenia:

  • A – punkt, z którego jest prowadzona obserwacja
  • B – punkt pośredni, względem którego określamy podniesienie względne
  • C – obserwowany punkt
  • dAB, dAC – odległości pomiędzy punktami A i B oraz A i C, mierzone wzdłuż powierzchni Ziemi (po łuku, w km)
  • R – promień Ziemi (km)
  • k – różnica współczynnika refrakcji
  • Pb(C), Pb(B) – podniesienie bezwzględne punktu (odpowiednio C i B) widzianego z punktu A (km)
  • Pw – podniesienie punktu C widzianego z punktu A względem punktu B (km)
Obliczenia mają na celu wyznaczenie wysokości, o którą zostaje pozornie podniesiony punkt C pod wpływem refrakcji atmosferycznej, widziany z punktu A. Wzrost współczynnika refrakcji o daną wartość daje zawsze taki sam efekt niezależnie od jego wartości początkowej, dlatego podajemy w arkuszu różnicę (przyrost) współczynnika. Podniesienie względne jest liczone względem pośredniego punktu B i ma zastosowanie do wyznaczenia podniesienia obiektu wystającego nad bliżej położonym terenem (który też ulega podniesieniu).
P_b(C)=\dfrac{d_{AC}^2k}{2R}\\ P_w=P_b(C)-\dfrac{d_{AC}d_{AB}k}{2R}
Wzór zawiera przybliżenia, ale jest wystarczająco dokładny dla odległości kilkuset kilometrów – dla 500 km i k=0,2 błąd wynosi 0,06%, dla 200 km i k=0,2 – 0,01%.

Wyprowadzenie wzorów

Wartość obniżenia punktu na powierzchni Ziemi względem płaszczyzny poziomej dla punktu, z którego jest prowadzona obserwacja, wynikającego z jej krzywizny, wynosi
b=R-Rcos\alpha=R-Rcos\dfrac{d}{R}
Geometrycznie efekt refrakcji atmosferycznej jest taki, jakby światło przebiegało w linii prostej, a Ziemia miała promień równy R’=R/(1-k). Można zatem obliczyć wartość b’ dla promienia Ziemi R’. Różnica b-b’ to wysokość refrakcyjnego podniesienia punktu, mierzona prostopadle do płaszczyzny poziomej dla punktu obserwacyjnego, a nie obserwowanego – jest to uproszczenie, pozostające jednak bez istotnego wpływu na wynik dla małych odległości, gdzie kąt zakrzywienia Ziemi jest mały.
P_b(C)=b-b'=R-Rcos\dfrac{d_{AC}}{R}-(R'-R'cos\dfrac{d_{AC}}{R'})
Dla małych kątów można zastosować przybliżoną zależność:
cos\alpha\approx 1-\dfrac{\alpha^2}{2}\\ P_b(C)\approx R-R(1-\dfrac{d_{AC}^2}{2R^2})-\dfrac{R}{1-k}+\dfrac{R}{1-k}(1-\dfrac{d_{AC}^2(1-k)^2}{2R^2})=\dfrac{d^2k}{2R}
Podniesienie punktu C względem punktu B obliczane jest następująco:
P_w=P_b(C)-P_b(B)\dfrac{d_{AC}}{d_{AB}}=\dfrac{d_{AC}^2k}{2R}-\dfrac{d_{AB}^2k}{2R}\dfrac{d_{AC}}{d_{AB}}=\dfrac{d_{AC}^2k}{2R}-d_{AC}d_{AB}\dfrac{k}{2R}

 

Podniesienie obserwatora odpowiadające wzrostowi refrakcji

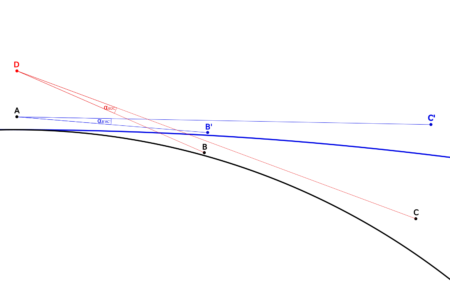
Oznaczenia:

  • A – punkt, z którego jest prowadzona obserwacja
  • B – punkt pośredni, względem którego określamy podniesienie względne
  • C – obserwowany punkt
  • D – punkt A po podniesieniu
  • B’, C’ – punkty B, C po zmianie promienia Ziemi symulującej refrakcję
  • xA, yA, xB, yB, xC, yC… – współrzędne punktów
  • dAB, dAC – odległości pomiędzy punktami A i B oraz A i C, mierzone wzdłuż powierzchni Ziemi (po łuku, w km)
  • R – promień Ziemi (km)
  • k – różnica współczynnika refrakcji
  • aCD, aBD… – współczynniki kierunkowe prostych zawierających odcinki CD, BD…
  • H – podniesienie obserwatora
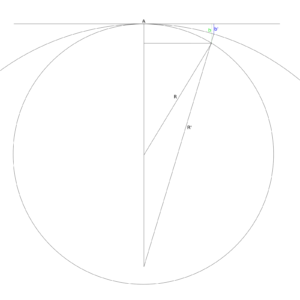
Czarny łuk oznacza powierzchnię Ziemi, niebieski – powierzchnię Ziemi o zmienionym promieniu, co symuluje refrakcję atmosferyczną. Celem obliczeń jest znalezienie wysokości, na jaką należy podnieść obserwatora, aby zachodziła równość miar kątów BDC i B’AC’.

Obliczenia są wykonywane w układzie współrzędnych kartezjańskich, którego środkiem jest środek Ziemi.
Polegają na znalezieniu wysokości, na jaką należy podnieść obserwatora powyżej punktu A, aby zachodziła równość miar kątów |BDC|=|B’AC’|. Kąty te są równe, gdy dDC−dDB=dAC’−dAB’.
Pominięto wysokości punktów n.p.m. ze względu na ich minimalny wpływ na wynik.

x_A=0\\ y_A=R\\ x_B=R\cdot\sin(d_{AB}/R)\\ y_B=R\cdot\cos(d_{AB}/R)\\ x_C=R\cdot\sin(d_{AC}/R)\\ y_C=R\cdot\cos(d_{AC}/R)
Geometrycznie efekt refrakcji atmosferycznej jest taki, jakby światło przebiegało w linii prostej, a Ziemia miała promień równy R’=R/(1-k). Punkty A, B’ i C’ położone na okręgu o promieniu R’ o środku w punkcie (0,R’-R) odpowiadają punktom A, B i C. Punkt A’ ma współrzędne punktu A.
x_{B'}=R'\cdot\sin(d_{AB}/R')\\ y_{B'}=R'\cdot\cos(d_{AB}/R')-(R'-R)\\ x_{C'}=R'\cdot\sin(d_{AB}/R')\\ y_{C'}=R'\cdot\cos(d_{AB}/R')-(R'-R)\\

|BDC|=|B'AC'|\\ a_{DC}-a_{DB}=a_{AC'}-a_{AB'}\\\\ \dfrac{y_C-y_D}{x_C-x_D}-\dfrac{y_B-y_D}{x_B-x_D}=\dfrac{y_{C'}-y_A}{x_{C'}-x_A}-\dfrac{y_{B'}-y_A}{x_{B'}-x_A}\\\\ x_D=0, x_A=0 \Rightarrow \dfrac{y_C-y_D}{x_C}-\dfrac{y_B-y_D}{x_B}=\dfrac{y_{C'}-y_A}{x_{C'}}-\dfrac{y_{B'}-y_A}{x_{B'}}\\\\ y_D=\dfrac{(\dfrac{y_{C'}-y_A}{x_{C'}}-\dfrac{y_{B'}-y_A}{x_{B'}})x_Bx_C+x_Cy_B-x_By_C}{x_C-x_B}\\\\ H=y_D-y_A=y_D-R
Podstawiając wzory na współrzędne poszczególnych punktów i stosując przybliżenia funkcji trygonometrycznych dla małych kątów, otrzymujemy uproszczony wzór:
cos\alpha\approx 1-\dfrac{\alpha^2}{2}, sin\alpha\approx \alpha \Rightarrow H\approx \dfrac{kd_{AB}d_{AC}}{2R}

Dla k=1 punkty A’, B’ i C’ są położone w płaszczyźnie poziomej dla punktu A. W celu uniknięcia dzielenia przez 0 przy obliczaniu R’ określono współrzędne punktów w następujący sposób:
x_A'=0\\ y_A'=y_B'=y_C'=R\\ x_B'=d_{AB}\\ x_C'=d_{AC}\\

 

Podniesienie punktu pod wpływem refrakcji – obliczenia na podstawie zdjęcia

Sytuacja jest podobna do wyznaczania minimalnego współczynnika refrakcji wymaganego do widoczności obiektu. Teraz nie znamy jednak współczynnika refrakcji, wiemy za to, na jaką wysokość obserwowany obiekt wystaje nad horyzontem z pomiarów dokonanych na zdjęciu. Refrakcyjne pozorne podniesienie punktu można określić jako różnicę wysokości, o jaką musiałby zostać podniesiony, aby w warunkach standardowych był widoczny na identycznej wysokości kątowej nad horyzontem. Przyjmując wyżej stosowane oznaczenia punktów A, B i C, musimy najpierw obliczyć wysokość punktu C, dla której z punktu A jest on widoczny dokładne za punktem B przy standardowej refrakcji. Następnie wyznaczenie podniesienia sprowadza się do odjęcia od tej wartości rzeczywistej wysokości bezwzględnej punktu C i dodania wysokości widocznej części obiektu zmierzonej na fotografii.

Oznaczenia:

  • hA, hB – wysokości n.p.m. punktów A, B, C (m)
  • hC – wysokość, jaką musiałby mieć punkt C, by z punktu A był widoczny za punktem B przy standardowej refrakcji atmosferycznej
  • dAB, dAC – odległości pomiędzy punktami A i B oraz A i C, mierzone wzdłuż powierzchni Ziemi (po łuku, w km)
  • R – promień Ziemi (km)
  • xA, yA, xB, yB, xC, yC – współrzędne punktów A, B i C
  • x0, y0 – współrzędne środka okręgu, na którym znajdują się punkty A, B i C
  • r – promień okręgu, na którym znajdują się punkty A, B i C (km) – jest równy r = R / k
  • k – standardowy współczynnik refrakcji równy 0,13
  • hCrz – rzeczywista wysokość n.p.m. punktu C
  • hCwid – wysokość widocznej części obserwowanego obiektu nad horyzontem, wyznaczona na fotografii
  • Pw – wartość pozornego refrakcyjnego podniesienia punktu C widzianego z punktu A względem punktu B (km)

Wartości hA, hB, hCrz, hCwid, dAB, dAC, R, k są znane.

1. Wyznaczenie współrzędnych punktów A, B:
x_A=0\\ y_A=R+h_A\\ x_B=(R+h_B)\cdot\sin(d_{AB}/R)\\ y_B=(R+h_B)\cdot\cos(d_{AB}/R)\\

2. Podstawiając współrzędne punktów A i B do równania okręgu, otrzymujemy układ równań:
\begin{cases} (x_0)^2+(y_A-y_0)^2=r^2\\ (x_B-x_0)^2+(y_B-y_0)^2=r^2 \end{cases}

3. Po przekształceniu powyższych równań otrzymujemy:
x_0=\dfrac{x_B^2+y_B^2-y_A^2+2y_0(y_A-y_B)}{2x_B}\\ \dfrac{(x_B^2+y_B^2-y_A^2)^2+4y_0(y_A-y_B)(x_B^2+y_B^2-y_A^2)+4y_0^2(y_A-y_B)^2}{4x_B^2}+y_0^2-2y_Ay_0+y_A^2-\frac{R^2}{k^2}=0
a następnie wyznaczamy x0 po podstawieniu y0.

4. Podstawiamy x0 i y0 do równania okręgu dla punktu C.
(x_C-x_0)^2+(y_C-y_0)^2=r^2
a następnie podstawiamy w nim:
x_C=(R+h_C)\cdot\sin(d_{AB}/R)\\ y_C=(R+h_C)\cdot\cos(d_{AB}/R)\\ r=\frac{R}{k}
i liczymy wartość hC.

5. Podniesienie refrakcyjne punktu C względem B jest równe:
P_w=h_C-h_C{rz}+h_{Cwid}

 

Lokalny współczynnik refrakcji atmosferycznej

Oznaczenia:

  • p – ciśnienie atmosferyczne (hPa)
  • t – temperatura powietrza (°C)
  • dt/dh – pionowy gradient temperatury powietrza (°C / 100 m)
  • k – współczynnik refrakcji

k=503 \cdot \dfrac{p}{(t+273,15)^2} \cdot (0,0343+0,01 \cdot \dfrac{dt}{dh})

Wyprowadzenie wzoru można znaleźć na stronie Waltera Bislina.

 

Arkusz 4. – kąt widzenia obiektywu i powiększenie obrazu

Kąt widzenia obiektywu

Oznaczenia:

  • f – ogniskowa (mm)
  • x – odległość obiektu od soczewki (mm)
  • y – odległość obrazu od soczewki (mm)
  • d – przekątna matrycy (mm)
  • a – długość dłuższego boku matrycy (mm)
  • b – długość krótszego boku matrycy (mm)
  • c – stosunek długości dłuższego boku matrycy do krótszego
  1. Z równania soczewki wynika następująca zależność:
    \dfrac{1}{f}=\dfrac{1}{x}+\dfrac{1}{y} \\ \\ y=\dfrac{fx}{x-f} \\ \\ \lim_{x\to\infty} y(x)=f
  2. Kąt widzenia obiektywu jest równy:
    \alpha=2\cdot arctg \dfrac{d}{2y}
    Dla dużych odległości do obiektu y≈f, zatem w przybliżeniu:
    \alpha=2\cdot arctg \dfrac{d}{2f}
  3. W arkuszu podajemy ekwiwalent ogniskowej dla matrycy pełnoklatkowej, więc posługujemy się wymiarami takiej matrycy – 36 x 24 mm.
    d=\sqrt{36^2+24^2}\text{ mm} \\ \\ \alpha=2\cdot arctg \dfrac{\sqrt{36^2+24^2}}{2f}
    Jest to kąt po przekątnej kadru. Kąty widzenia wzdłuż obu boków matrycy zależą od stosunku długości jej boków i liczone są analogicznie, lecz zamiast d podstawiamy długość boku matrycy.
    Dla matrycy 3:2 wystarczy podać wymiary matrycy pełnoklatkowej (36 mm i 24 mm). W przypadku innych proporcji boków wykonywane są obliczenia oparte o twierdzenie Pitagorasa.
    c=\dfrac{a}{b} \\ \\ d^2=a^2+b^2
    Po przekształceniu powyższych równań otrzymujemy:
    a=c \cdot \sqrt{\dfrac{d^2}{c^2+1}} \\ \\ b=\sqrt{\dfrac{d^2}{c^2+1}}

 

Wielkość obiektu widocznego na zdjęciu

Obliczenia wykorzystują kąt widzenia wzdłuż dłuższego boku matrycy.
Oznaczenia:

  • α – kąt widzenia obiektywu dla dłuższego boku matrycy w radianach
  • a – liczba pikseli na dłuższym boku matrycy
  • d – odległość od obiektu w kilometrach
  • l – wielkość obiektu na zdjęciu w pikselach
  • L – rzeczywista wielkość obiektu w metrach

L=\dfrac{l}{a} \cdot \alpha \cdot 1000d

Powiększenie obrazu widzianego w wizjerze
Obraz widziany przez obiektyw o ogniskowej 50 mm i wizjer o powiększeniu 1x ma wielkość taką, jak widziany gołym okiem (powiększenie 1x).
Powiększenie widzianego w wizjerze obrazu jest więc równe stosunkowi kąta widzenia dla obiektywu 50 mm do kąta widzenia użytego obiektywu, pomnożonemu przez powiększenie wizjera.

Oznaczenia:

  • α – kąt widzenia obiektywu (obliczony jak wyżej dla przekątnej matrycy w radianach)
  • α(50) – kąt widzenia obiektywu o ogniskowej 50 mm w radianach
  • f – ogniskowa obiektywu w mm
  • fekw – ekwiwalent ogniskowej dla formatu 35 mm (pełnej klatki) w mm
  • c – mnożnik ogniskowej (crop factor) będący ilorazem przekątnej matrycy pełnoklatkowej i matrycy aparatu
  • n – powiększenie wizjera
  • N – powiększenie obrazu widzianego w wizjerze

N=\dfrac{\alpha(50)}{\alpha} \cdot n=\dfrac{2\cdot arctg \dfrac{\dfrac{\sqrt{36^2+24^2}}{c}}{2 \cdot 50}}{2\cdot arctg \dfrac{\dfrac{\sqrt{36^2+24^2}}{c}}{2f}} \cdot n=\dfrac{arctg \dfrac{\sqrt{36^2+24^2}}{100c}}{arctg \dfrac{\sqrt{36^2+24^2}}{2cf}}\cdot n \\ \\ \\ N\approx\dfrac{arctg \dfrac{\sqrt{36^2+24^2}}{100}}{arctg \dfrac{\sqrt{36^2+24^2}}{2f}} \cdot n
Jeśli zamiast rzeczywistej ogniskowej obiektywu podajemy jego ekwiwalent dla formatu 35 mm, trzeba obliczyć ogniskową rzeczywistą, dzieląc ekwiwalent przez mnożnik ogniskowej.
f_{ekw} =\dfrac{f}{c} \\ \\ \\ N=\dfrac{arctg \dfrac{\sqrt{36^2+24^2}}{100c}}{arctg \dfrac{\sqrt{36^2+24^2}}{\dfrac{2cf_{ekw}}{c}}}\cdot n = \dfrac{arctg \dfrac{\sqrt{36^2+24^2}}{100c}}{arctg \dfrac{\sqrt{36^2+24^2}}{2f_{ekw}}}\cdot n
Przyjęto następujące wartości mnożnika ogniskowej:

  • pełna klatka – 1
  • APSC Sony/Pentax, DX Nikon – 1,5
  • APSC Canon – 1,6
  • 4/3” – 2
  • 1” – 2,72

 

Powiększenie obrazu widzianego na ekranie aparatu

Oznaczenia:

  • α – kąt widzenia obiektywu (obliczony dla przekątnej matrycy)
  • β – kąt widzenia przekątnej ekranu
  • d – przekątna ekranu (w calach)
  • d’ – przekątna obrazu widocznego na ekranie (w calach)
  • f – ekwiwalent ogniskowej obiektywu dla formatu 35 mm (w milimetrach)
  • m – stosunek długości dłuższego boku matrycy do krótszego
  • e – stosunek długości dłuższego boku ekranu do krótszego
  • l – odległość oka od ekranu (w metrach)
  • n – powiększenie cyfrowe obrazu na ekranie
  • N – powiększenie widzianego obrazu

Powiększenie jest w tym przypadku równe ilorazowi kąta widzenia obrazu wyświetlanego na ekranie i kąta widzenia, który obejmuje obraz wyświetlany na ekranie.
N=\dfrac{n\beta}{\alpha} \\ \alpha=2\cdot arctg \dfrac{\sqrt{36^2+24^2}}{2f} \\ \beta=2\cdot arctg \dfrac{0,0254d'}{2l}
Kąt widzenia obiektywu dla rzeczywistej ogniskowej można obliczyć, wstawiając do powyższego wzoru ogniskową pomnożoną przez mnożnik ogniskowej (crop factor) dla matrycy danego aparatu.
Jeśli stosunki długości boków ekranu i matrycy różnią się, przekątna obrazu na ekranie jest mniejsza od przekątnej ekranu. Należy zatem obliczyć d’.
Dla m=n:
d'=d
Dla m>n:
d'=d\cdot\sqrt{\dfrac{\frac{1}{m^2}+1}{\frac{1}{n^2}+1}}
Dla m<n:
d'=d\cdot\sqrt{\dfrac{m^2+1}{n^2+1}}